Гидравлический расчет трубопроводов
-
Гидростатика
-
Применение уравнения Бернулли
-
Истечения жидкости через отверстия
-
Гидравлический расчет трубопроводов
-
Гидромашины
-
Гидроприводы
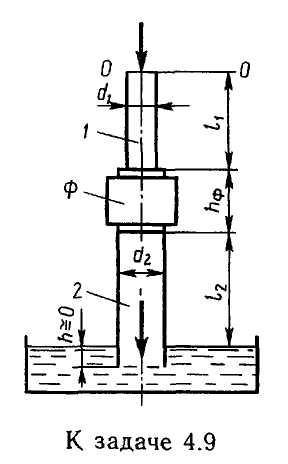
Задача 4.17
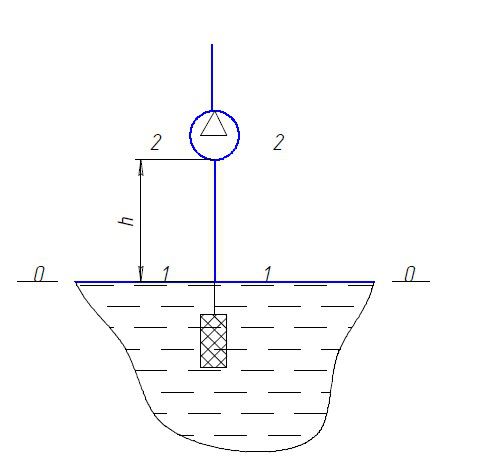
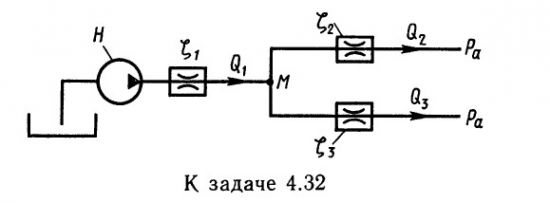
Автор страницы: admin

Задача 4.17


Автор страницы: admin