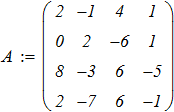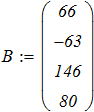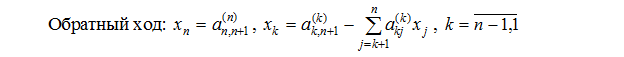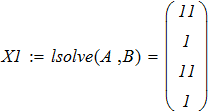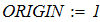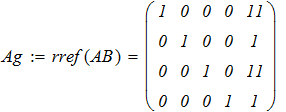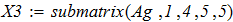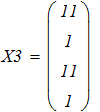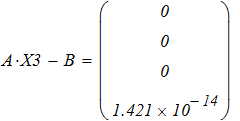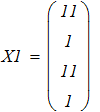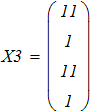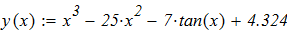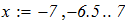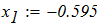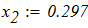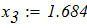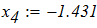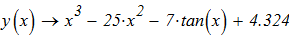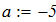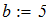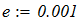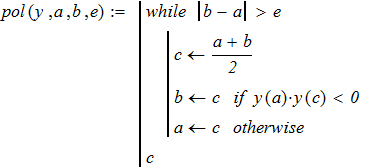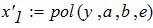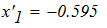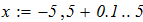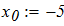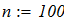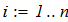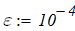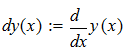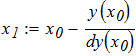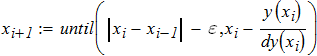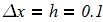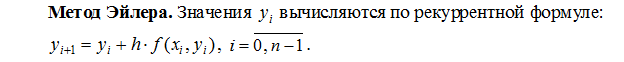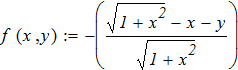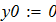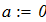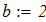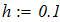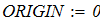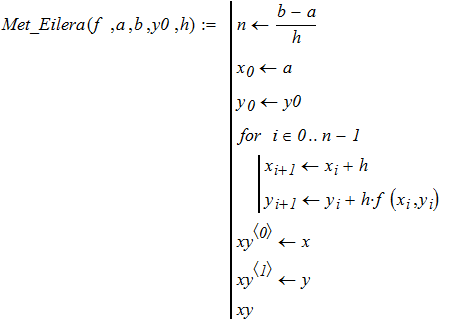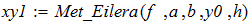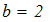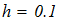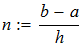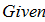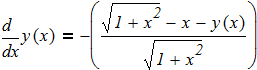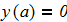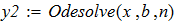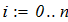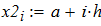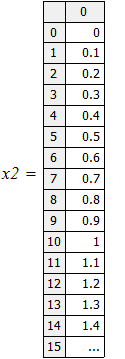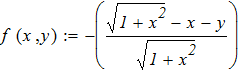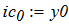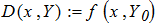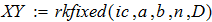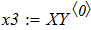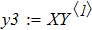Артикул: матмод1
Автор решения: admin
в каталог Задача 1. Решение задачи состоит в решении системы линейных уравнений, запись которых в матричной форме имеет вид AхX = B . Для заданных матриц A и B…
Задача 1.
Решение задачи состоит в решении системы линейных уравнений, запись которых в
матричной форме имеет вид AхX = B . Для заданных матриц A и B выполнить решение
системы линейных уравнений следующими способами:
1. Решить систему линейных уравнений, используя функцию lsolve(A, B)
математического пакета MathCAD.
2. Решить систему уравнений методом Крамера или методом Гаусса в зависимости от
варианта.
3. Сравнить полученные разными способами результаты вычислений корней системы
уравнений.
Исходные данные
Задача 2.
Решить нелинейное уравнение, выбрав его в соответствии с вариантом:
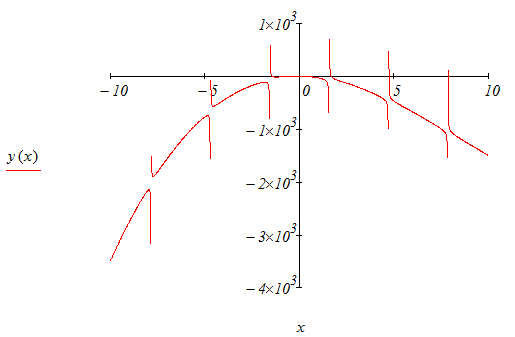
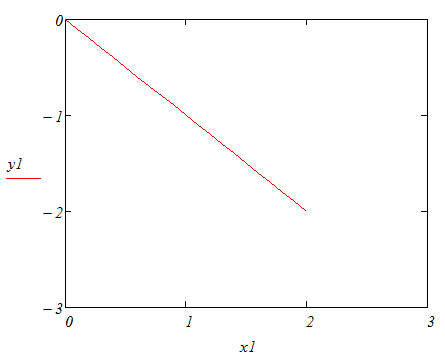
1. построить график функции, для проведения предварительного анализа;
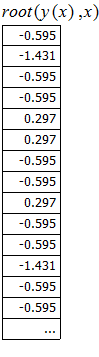
2. с использованием функции root (F(x), x, a, b) математического пакета программ
MathCAD.
3. используя известные вычислительные алгоритмы в соответствии с вариантом (методом
половинного деления, методом итераций, методом Ньютона и др.).
4. Сравнить полученные результаты вычислений.
Исходные данные
Задача 3.
Составить программы для численного интегрирования дифференциального уравнения
dy/dx = f (x, y) при известых начальных условиях y0 = y(x0). Интегрирование выполнить в цикле от х=х0, до х = хk с шагом интегрирования h=0.1
Решение уравнения выполнить:
1. методом Эйлера
2. используя встроенные функции MathCAD и вычислительный блок Given.
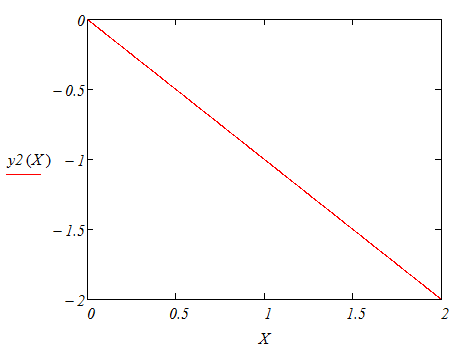
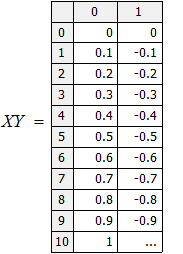
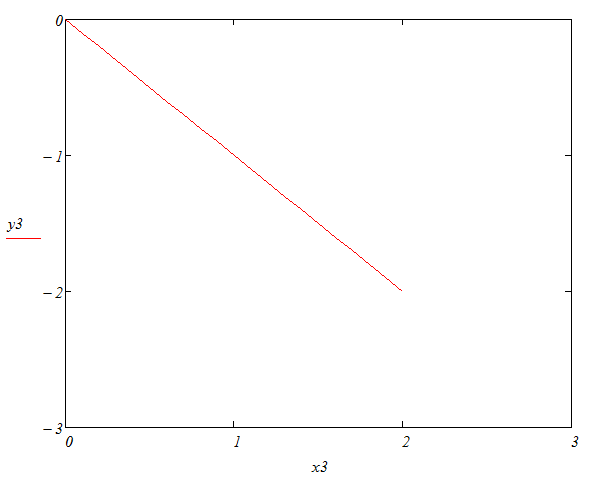
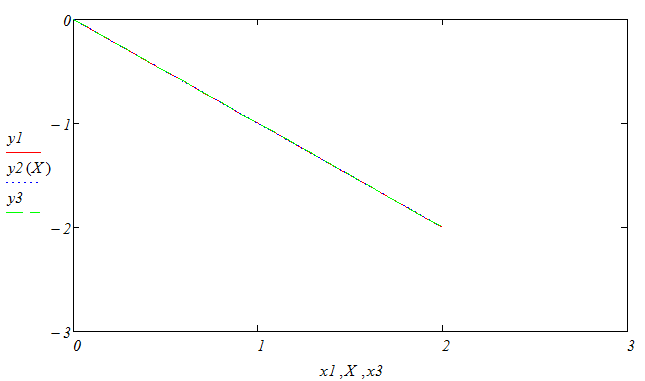
Результаты расчетов вывести в виде таблицы и в виде графиков (в одном поле построения).
Сравнить результаты, полученные при решении задачи разными методами.
Исходные данные
Важно!
Если ваша задача соответствует исходным данным указанным выше для задач 1, 2 и 3, то для заказа следует нажать "Добавить в корзину" и в окне оплаты в комментариях указать свой вариант для каждой задачи. Либо написать мне |через сайт| в контакте| на почту|
Если у вас значения для расчета произвольные - нажимайте "заказать подобную задачу" и в окне заказа указывайте свои исходные данные. Либо высылайте файл с заданием.
Решение задачи
Задача 1.
Решение задачи состоит в решении системы линейных уравнений, запись которых в
матричной форме имеет вид A*X = B . Для заданных матриц A и B выполнить решение
системы линейных уравнений следующими способами:
1. Решить систему линейных уравнений, используя функцию lsolve(A, B)
математического пакета MathCAD.
2. Решить систему уравнений методом Крамера или методом Гаусса в зависимости от
варианта.
3. Сравнить полученные разными способами результаты вычислений корней системы
уравнений.
3. Аналиируя полученные ответы во всех представленных способах расчета систем линейных уравнений, приходим к выводу, что искомые элементы величины Х совпадают.
Задача 2.
1. Решить нелинейное уравнение, выбрав его в соответствии с вариантом:
построить график функции, для проведения предварительного анализа;
2. С использованием функции root (F(x), x, a, b) математического пакета программ
MathCAD.
3. Используя известные вычислительные алгоритмы в соответствии с вариантом (методом
половинного деления, методом итераций, методом Ньютона и др.).
4. Сравнить полученные результаты вычислений.
3. Используя известные вычислительные алгоритмы в соответствии с вариантом (методом
половинного деления, методом итераций, методом Ньютона и др.).
4. Сравнивая различные способы нахождения корней в математическом пакете Mathcad приходим к выводу, что полученный результат во всех случаях получился почти одинаковым. Преимуществом функции root является возможность нахождения сразунескольких значений корней, если таковые имеются.
Задача 3.
Решение дифференциальных уравнений.
Задание.
Составить программы для численного интегрирования дифференциального уравнения
при известных начальных условиях 
. Интегрирование выполнить в цикле от 
до 
с шагом интегрирования 
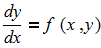
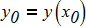
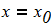
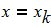
Решение уравнения выполнить:
1. Методом Эйлера.
2. Используя встроенные функции MathCAD и вычислительный блок Given.
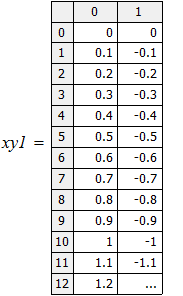
Результаты расчетов вывести в виде таблицы и в виде графиков (в одном поле построения). Сравнить результаты, полученные при решении задачи разными методами.
