Методология моделирования систем (Транспортная задача)
| Вариант 1 | Вариант 2 | Вариант 3 |
| Вариант 4 | Вариант 5 | Вариант 6 |
| Вариант 7 | Вариант 8 | Вариант 9 |
Вариант 1. Минимизировать затраты на перевозку грузов с заводов-производителей (Белоруссия, Урал, Украина) на торговые склады (Казань, Рига, Воронеж, Курск, Москва). Учесть возможности поставок каждого из производителей при максимальном удовлетворении запросов потребителей. Затраты на перевозки от заводов-изготовителей к складам приведены в таблице:
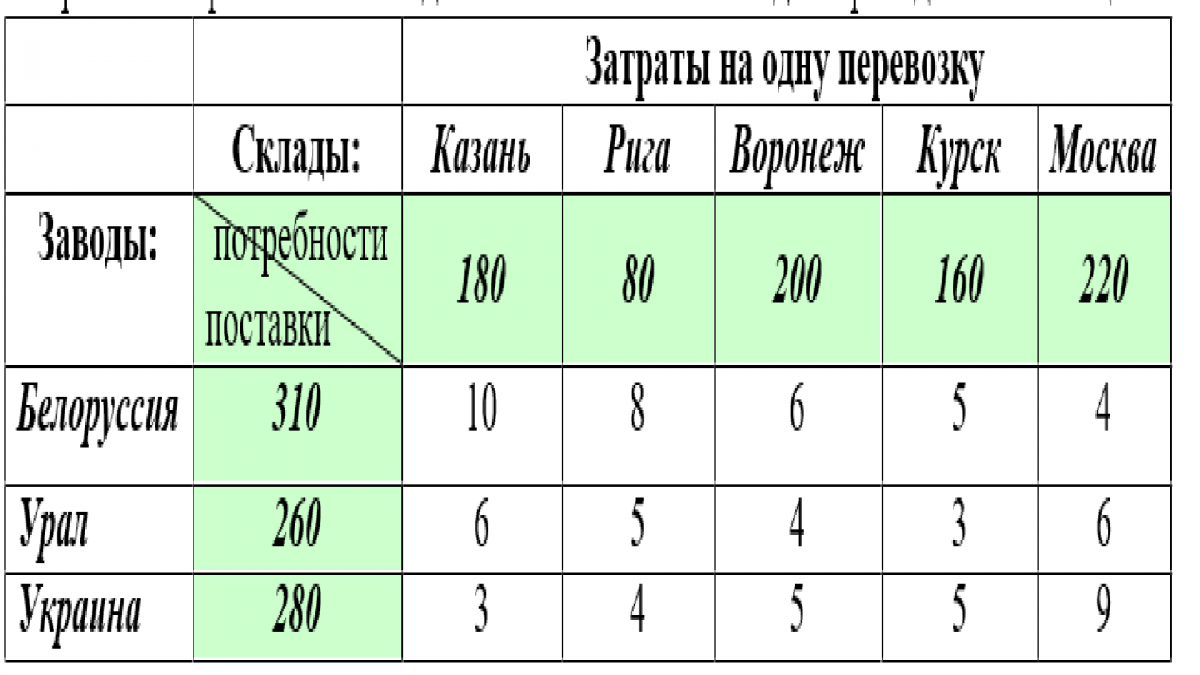
Вариант 2. Бетон, производимый на заводах А и В, нужно развозить по трем стройплощадкам N1, N2 и N3. Известны потребности стройплощадок в бетоне, запасы бетона на каждом заводе и затраты на перевозку 1 тонны бетона от каждого завода до каждой стройплощадки. Требуется составить такой план перевозок, который обеспечивал бы наименьшие затраты.
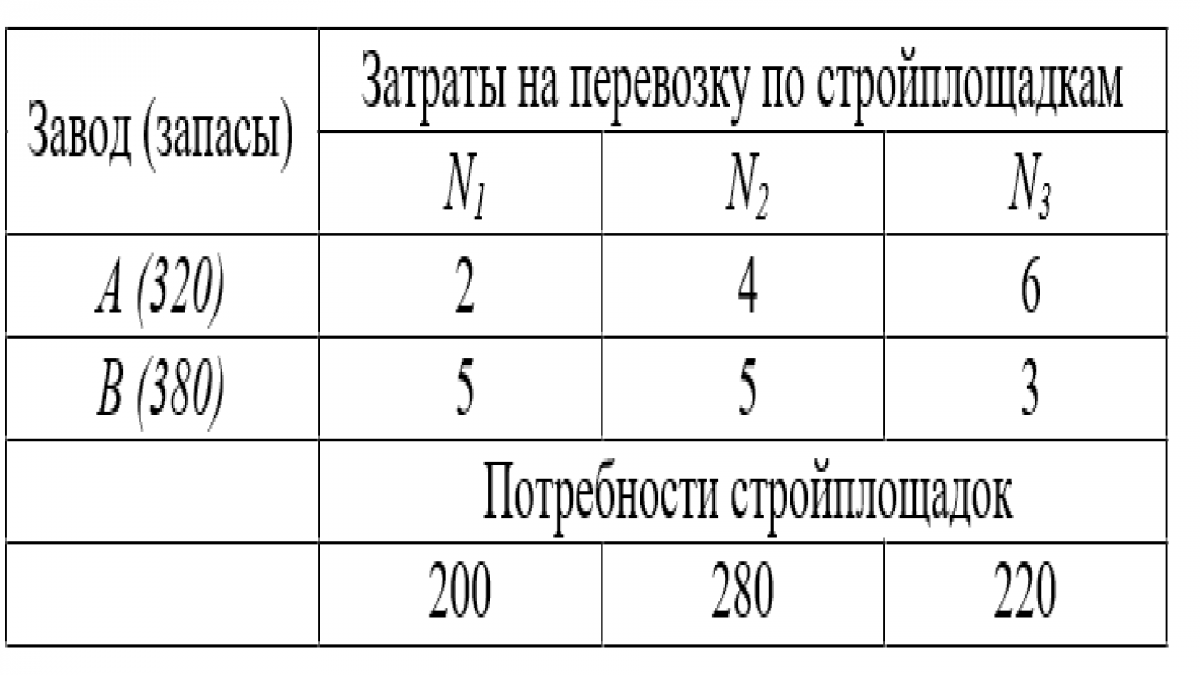
Вариант 3. Составьте оптимальный план проведения экскурсионных поездок в следующей ситуации. Возможно профинансировать поездки из пяти районов области (1,2,3,4,5) в три города (X, Y, Z). Количество участников экскурсий таково:
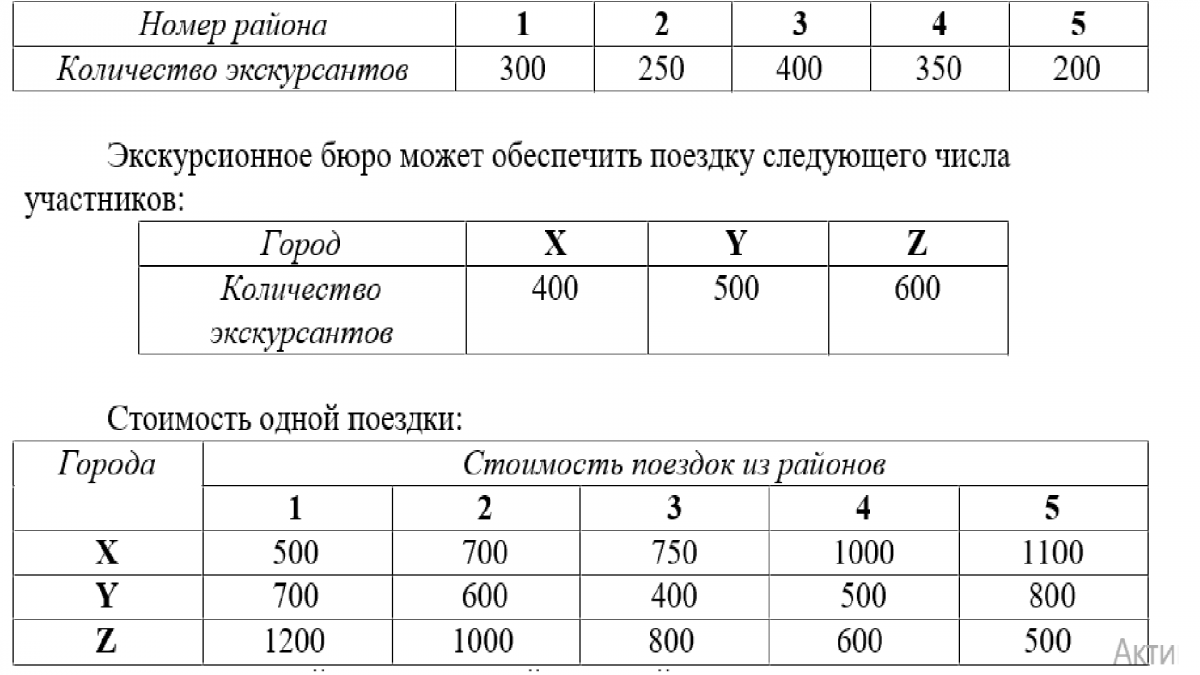
Составить такой план экскурсий, который:
-позволяет каждому из числа намеченных для участия в экскурсии побывать на ней;
-удовлетворяет условию, определяющему общее число экскурсантов, едущих в каждый из городов
-обеспечивает максимально низкие суммарные расходы финансирующей стороны.
Вариант 4. Для строительства дорог необходим гравий в количестве 130, 220, 60 и 70 единиц, который может быть поставлен из карьеров. Запасы гравия в этих карьерах составляют 120, 280 и 160 единиц соответственно, а тарифы перевозок представлены матрицей
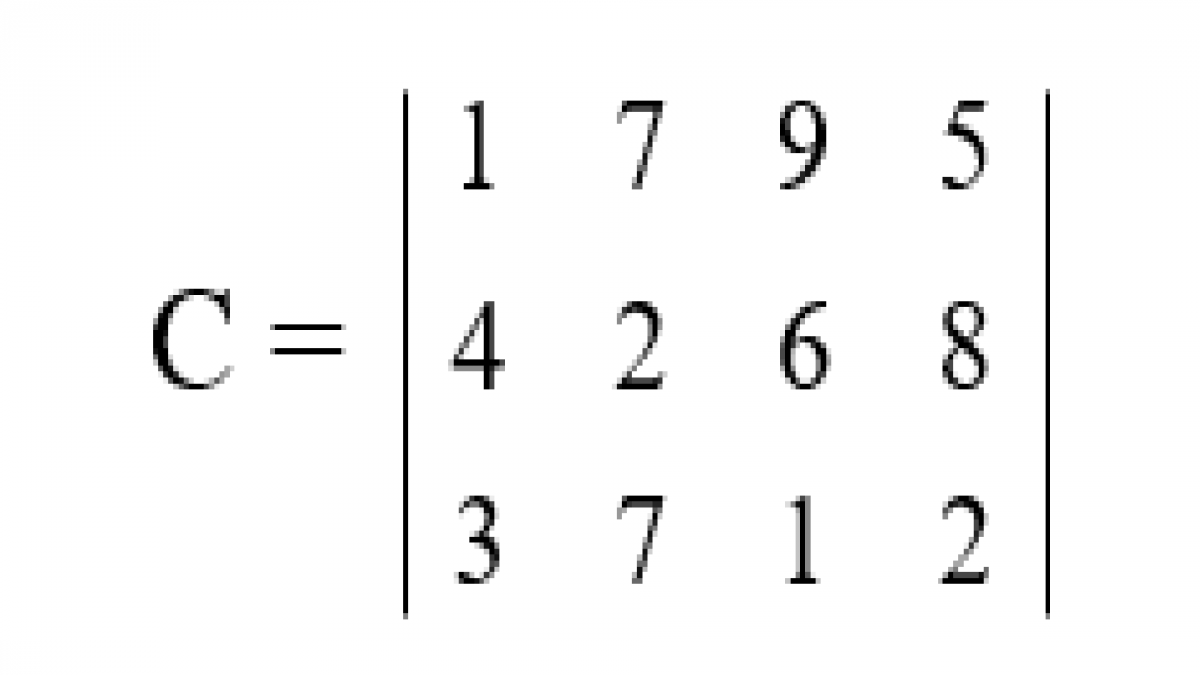
Составьте такой план перевозок гравия, при котором потребности в нем каждой из строящихся дорог были полностью удовлетворены при минимально возможной общей стоимости перевозок.
Вариант 5. Найдите такой план перевозок продукции с четырех складов пяти
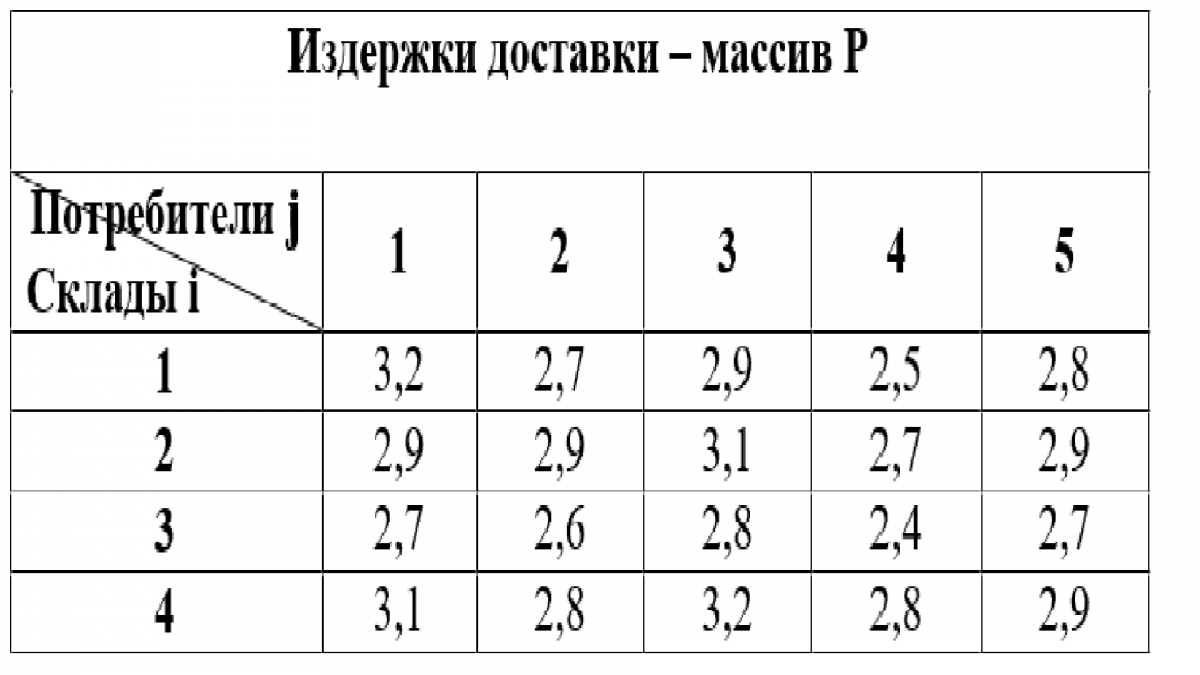
потребителям, который требовал бы минимальных затрат.
Наличие на складе продукции (начиная с 1 склада по четвертый) - 250, 220, 280, 250. Потребителям необходимо доставить товаров на сумму (с 1 потребителя до 5) – 190, 210, 220, 230 и 150.
Вариант 6. Найдите оптимальный план загрузки вагонов контейнерами трех типов: длиной 3, 5 и 7 м при длине вагона – 14 м. Рассмотрите 6 возможных вариантов загрузки – ячейки С7:Е12.
Для контроля суммарной длины контейнеров в вагоне созданы колонки «Проверка на max» и «Проверка на min». (Введите в ячейку G7 формулу =ЕСЛИ(G$5>=F7; «погрузка»; «нет»), в ячейку H7 – формулу =ЕСЛИ(G$5>=F7+C$5; «свободно»; «погрузка»), которые скопируйте в диапазон G8:H12. Таким образом, суммарная длина контейнеров, загружаемых в вагон, не
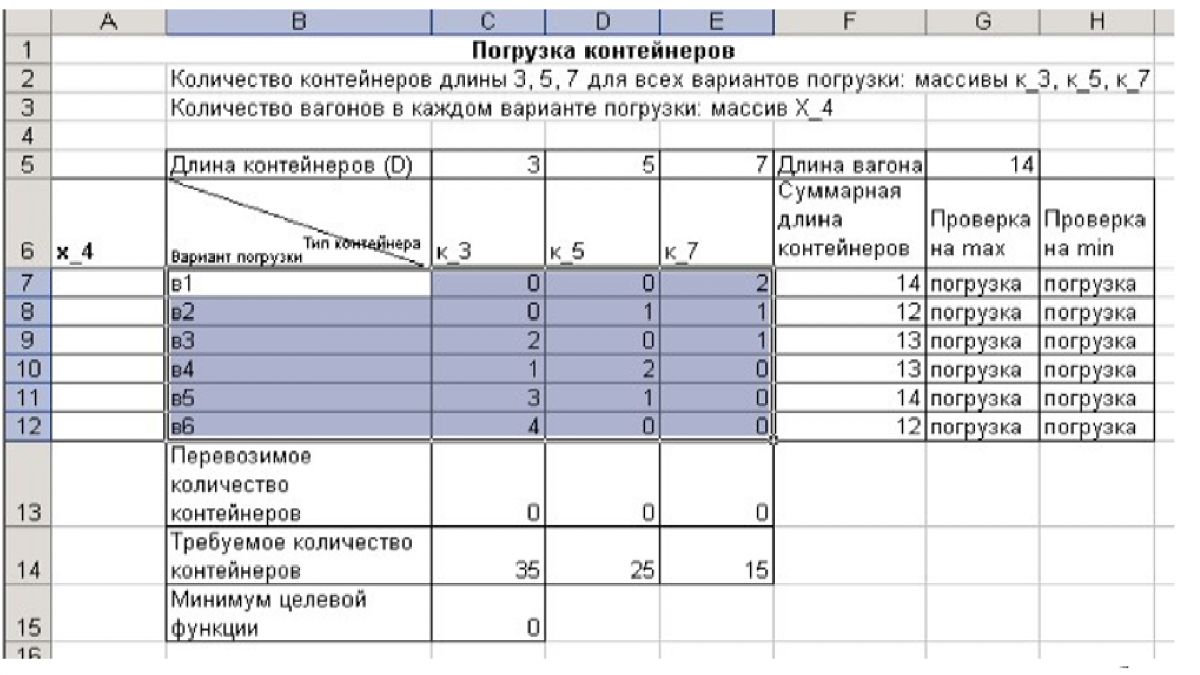
должна превышать его длины, а также позволять загружать вагон еще хотя бы одним контейнером.)
Вариант 7. Организуйте оптимальный план перевозок пассажиров самолетами трех типов по четырем направлениям. Себестоимость перевозок и все остальные необходимые для решения задачи данные приводятся в таблице.
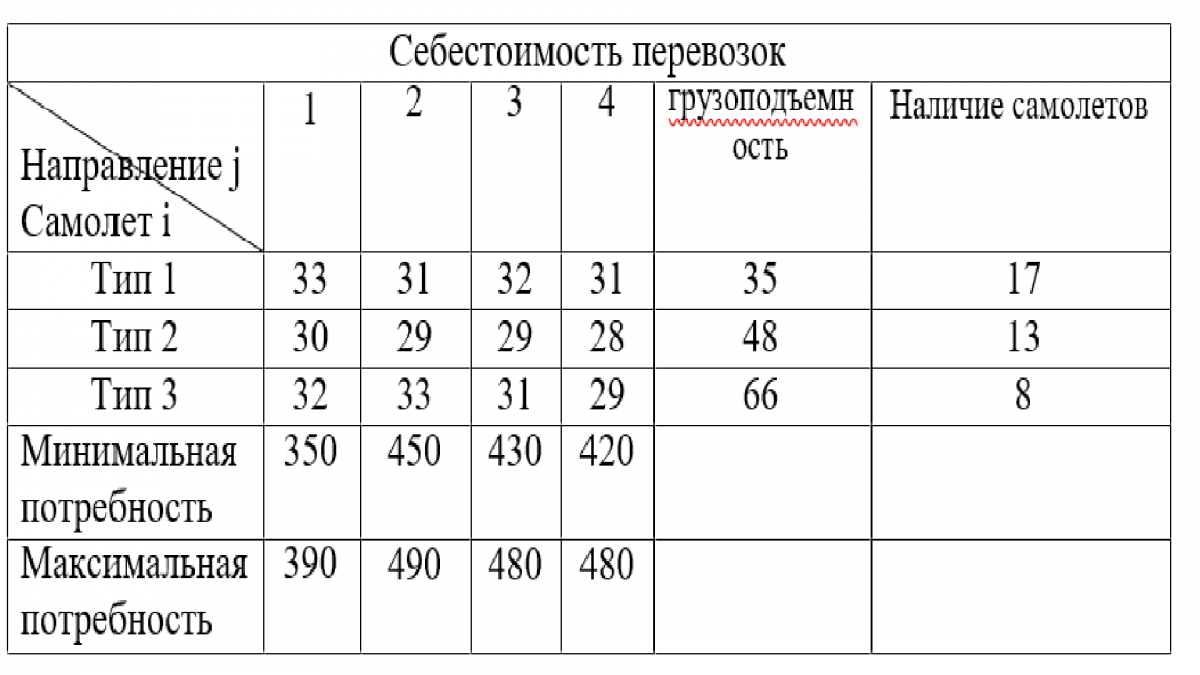
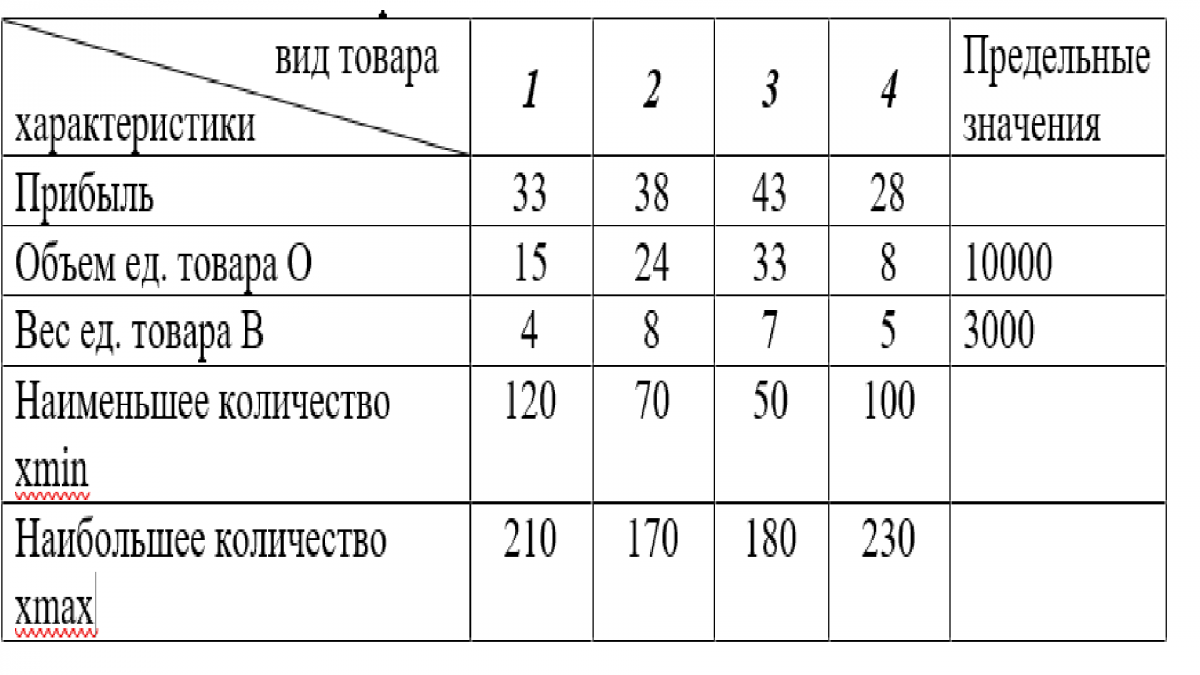
Вариант 8. Найдите оптимальный план загрузки контейнера товарами четырех видов, учитывая прибыль от реализации каждого вида товара, его вес и занимаемый в контейнере объем.
Вариант 9. С трех складов требуется развезти закупленные в них грузы в объемах 30, 40 и 50 тонн потребителям в два пункта доставки в объеме 40 и 80 тонн соответственно. Цена перевозки единицы груза с каждого склада в каждый пункт доставки известна и приведена в таблице:
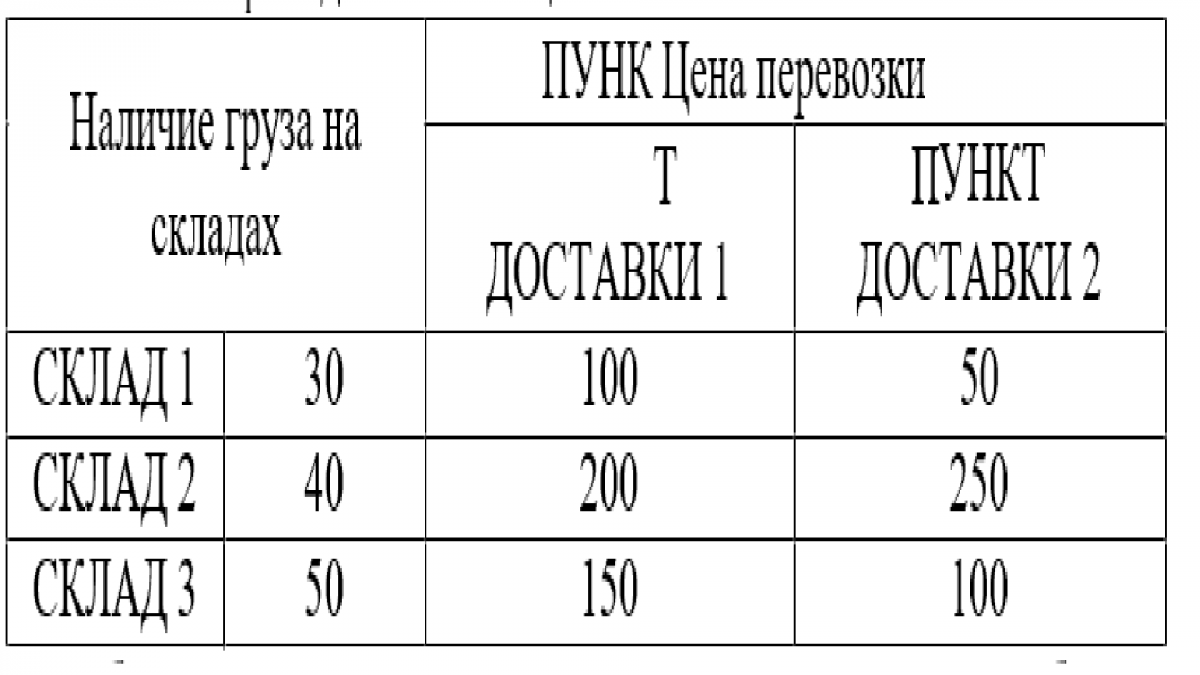
Определить объемы перевозок со складов в пункты доставки так, чтобы стоимость транспортировки была минимальной.
Автор страницы: admin 2




