Электрооборудование и электротехнологии, теплоэнергетика и теплотехника (Методичка 2016г)
<в каталог
Студент выполняет вариант контрольной работы, совпадающий с последней цифрой его учебного шифр. При этом, если предпоследняя цифра учебного шифра есть число нечетное (1, 3, 5, 7, 9), то номера задач для соответствующего варианта даны в таблице 1. Если же предпоследняя цифра учебного шифра есть число четное или ноль (0, 2, 4, 6, 8), то номера задач приводятся в таблице 2.
КОНТРОЛЬНАЯ РАБОТА №1 ТАБЛИЦА
1. Решить систему линейных уравнений по формулам Крамера иметодом Гаусса.
Исходные данные по вариантам
2. Определить тип кривой, найти ее параметры; определить угловой коэффициент прямой. Найти точки пересечения данных линий и сделать чертеж.
Исходные данные по вариантам
3. Даны координаты вершин пирамиды АВСD. Требуется:
1) записать векторы АВ, АС, АD в системе орт i j k и найти модули этих векторов;
2) найти угол между векторами АВ и АС ;
3) найти проекцию вектора АD на вектор АВ ;
4) найти площадь грани АВС;
5) найти объем пирамиды АВСD;
6) составить уравнение ребра АС;
7) составить уравнение грани АВС.
Исходные данные по вариантам
4. Провести полное исследование функции методами дифференциального исчисления и построить ее график.
Исходные данные по вариантам
КОНТРОЛЬНАЯ РАБОТА №2 ТАБЛИЦА
5. Решить систему двух линейных уравнений в области комплексных чисел по формулам Крамера. Найденные
z1, z2 , z = z1 + z2 , u = z1 - z2 изобразить на комплексной плоскости; z1, z2 , v = z1 * z2 , w = z1 : z2 записать в показательной и тригонометрической формах.
Исходные данные по вариантам
6. а) Вычислить площадь фигуры, ограниченной заданными параболами.
б) Найти объем тела, образованного вращением вокруг оси Ох фигуры, расположенной в первом квадранте и ограниченной заданными параболой, прямой и осью Ох.
Исходные данные по вариантам
7. Классическим методом найти частное решение системы дифференциальных уравнений, удовлетворяющее начальным условиям.
Исходные данные по вариантам
8. Найти интервал сходимости степенного ряда и выяснить вопрос о сходимости ряда на концах интервала.
Исходные данные по вариантам
9. Найти разложение в степенной ряд по степеням х решения дифференциального уравнения (записать три первых отличных от нуля члена этого разложения).
Исходные данные по вариантам
КОНТРОЛЬНАЯ РАБОТА №3 ТАБЛИЦА
10. Дана функция двух переменных z(x; y) . Найти:
1) экстремум функции z(x; y) ;
2) gradz в точке А(1; –2);
3) наибольшую скорость возрастания z(x; y) точке А(1; –2).
Исходные данные по вариантам
11. Найти поток векторного поля F через полную поверхность пирамиды S , образованной данной плоскостью 4 S и координатными плоскостями 1 S , 2 S , 3 S в направлении внешней нормали к ее поверхности, применив теорему Остроградского–Гаусса.
Исходные данные по вариантам
12. Установить независимость от пути интегрирования криволинейного
интеграла и вычислить работу, совершаемую переменной силой F по контуру, связывающему точки М(1; 2) и N(3; 5).
Исходные данные по вариантам
13. Дано векторное поле V и точки M1, M2 и M3 .
1) Показать, что поле V – потенциальное.
2) Найти потенциал U(x; y; z) , если известно, что U(0;0;0) = n, где n –номер варианта.
3) Найти работу поля между точками M1 и M2 , M2 и M3 , M3 и M1 и найти циркуляцию по контуру M1M2 M3 M1.
Исходные данные по вариантам
14. Найти вероятность безотказной работы участка цепи, если известно, что каждый i -ый элемент работает независимо от других с вероятностью pi ( i =1,2,3,4,5).
p1 = 0,6, p2 = 0,7, p3 = 0,8, p4 = 0,5, p5 = 0,9
Исходные данные по вариантам
КОНТРОЛЬНАЯ РАБОТА №4 ТАБЛИЦА
15. Разложить заданную функцию f (x) в ряд Фурье по синусам на отрезке [0;π] и построить результирующую первых двух гармоник полученного ряда.
Исходные данные по вариантам
16. Две независимые дискретные случайные величины Х и У заданы своими законами распределения. Найти математическое ожидание и дисперсию для случайной величины Z=3X-2Y
Исходные данные по вариантам
17. Предполагается, что случайные отклонения контролируемого размера детали, изготовленной станком-автоматом, от проектного размера, подчиняются нормальному закону распределения со средним квадратическим отклонением σ (мм) и математическим ожиданием а = 0. Деталь, изготовленная станком-автоматом, считается годной, если отклонение ее
контролируемого размера от проектного по абсолютной величине не превышает т (мм). Сколько процентов годных деталей изготовляет станок?
Исходные данные по вариантам
18. Произведена выборка 90 деталей из текущей продукции токарного автомата. Проверяемый размер деталей X измерен с точностью до одного миллиметра. Результаты измерений приведены в таблице.
-
Построить статистическое распределение выборки.
-
Выполнить точечные оценки среднего значения x и дисперсии D( X ) случайной величины X .
-
Построить гистограмму относительных частот, установив статистический (эмпирический) закон распределения.
-
На том же чертеже построить кривую нормального распределения с параметрами a = x и
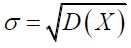и проанализировать, хорошо ли статистические данные описываются нормальным законом распределения и проверить правило "3σ"
