Механика 3 задачи (техносферная безопасность)
в каталог
Таблицы к готовым задачам → Задача 1 Задача 2 Задача 3
СТАТИКА
Задача 1
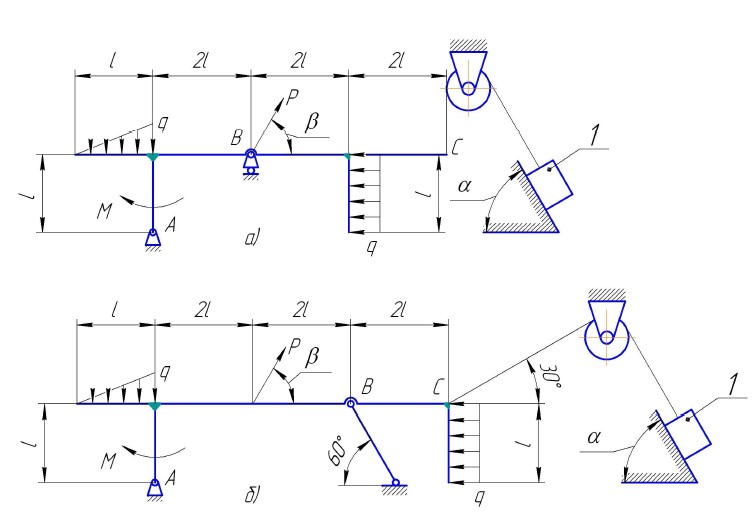
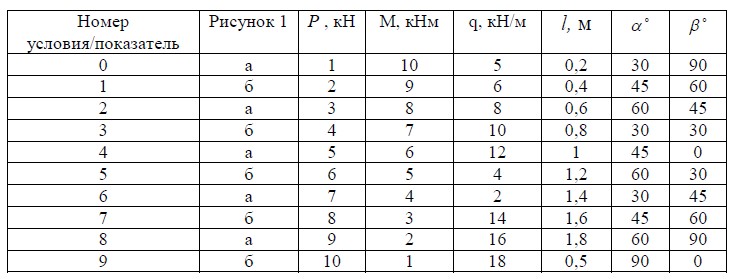
Жесткая рама рис.1 закреплена в точке А шарнирно, а в точке В
прикреплена или к невесомому стержню с шарнирами на концах, или к
шарнирной опоре на катках.
В точке С к раме привязан трос, перекинутый через блок и усилие со
стороны груза 1 скользящего по наклонной поверхности, масса груза 1 - 200 кг,
коэффициент трения f=0,1. На раму приложена распределенная нагрузка q
(кН/м), сосредоточенная сила Р (кН), действует пара сил с моментом М (кН м),
длина участков l (м), значения которых указаны в таблице.
Определить реакции связей в опорах точки А и В, вызываемые
действующими нагрузками. При решении учесть, что натяжение обеих ветвей
нити, перекинутой через блок одинаковы, т.е. трением пренебречь.
Указания. Задача 1 – на равновесие тела (бруса), находящихся под
действием плоской системы сил. Задачу решаем в два этапа. Первый:
расчленить систему и рассмотреть, равновесие груза 1, для определения
натяжения нити, составив для этого два уравнения равновесия. Второй:
рассмотреть равновесие всей системы, без груза, учтя при изображении
реакций в нити закон о равенстве действия и противодействия, составив для
неё три уравнения равновесия.
Решенные задачи к данному разделу
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 |
| Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант 0 |
КИНЕМАТИКА
Задача 2
Определение скорости и ускорения точки по заданным уравнениям ее
движения
По заданным уравнениям движения точки М установить вид ее
траектории и для момента времени t=t1 (с) наитии положение точки на
траектории, ее скорость, полное, касательное и нормальное ускорения, а также
радиус кривизны траектории.
Необходимые для решения данные приведены в таблице.

Готовые варианты по второму разделу
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 |
| Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант 10 |
| Вариант 11 | Вариант 12 | Вариант 13 | Вариант 14 | Вариант 15 |
ДИНАМИКА
Задача 3
Применения теоремы об изменении кинетической энергии.
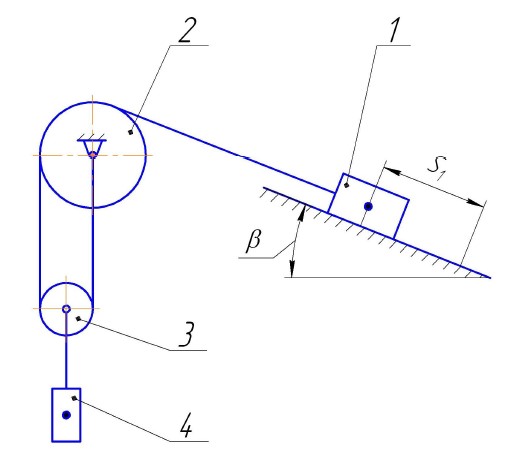
Механическая система (рис.3) под действием сил тяжести приходит в
движение из состояния покоя. Учитывая трение скольжения тела 1
(коэффициент трения f), пренебрегая другими силами сопротивления и массами
нитей, предполагаемых нерастяжимыми, определить скорость тела 1 в тот
момент, когда пройденный им путь станет равным S (см. рис).
При решении заданий № 1, 5, 7, 9 радиус блоков принять R2=2R, R3=R
(R=0,2м).
Решенные задачи к данному разделу
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 |
| Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант 0 |




