Физика. Контрольная работа №3. Сибирский государственный университет телекоммуникаций и информатики (УрТИСИ СибГУТИ)

в каталог

Варианты заданий для контрольной работы № 3.

Задачи для выполнения домашней контрольной работы №3

1. Материальная точка массой 25 г совершает гармонические колебания с амплитудой 10 см и частотой 1 Гц. Чему равна ее кинетическая энергия и действующая на нее сила в тот момент, когда ее смещение от положения равновесия равно 5 см?

2. Написать уравнение гармонического колебательного движения, если максимальное ускорение точки равно a_max = 49.3 см/с², период колебаний Т=2с и смещение точки от положения равновесия в начальный момент времени х₀=25 мм.

3. Начальная фаза гармонического колебания j₀ = 0. При смещении точки от положения равновесия х₁ = 2.4 см скорость точки v₁ = 3 м/с, а при смещении х₂ = 2.8 м ее скорость v₂  = 2 м/с. Найти амплитуду А и период Т этого колебания.

4. Математический маятник, состоящий из нити длиной l = 0,5 м и свинцового шарика массой m = 50 г совершает гармонические колебания с амплитудой x₀ = 5 см. Определить: 1) скорость шарика при прохождении им положения равновесия; 2) максимальное значение возвращающей силы.

5. Физический маятник представляет собой тонкий однородный стержень массы m длиной l. Определить частоту колебаний маятника, если точка подвеса находится от центра масс на расстоянии x. Момент стержня относительно середины I = ml²/12.

6. Коэффициент жесткости пружины равен 10 Н/см, а масса груза 1 кг. Каковы были начальные значения смещения и скорости груза, если амплитуда колебаний 5 см, а начальная фаза 60°.

7. Шарик массой 0.01 кг совершает гармонические колебания с амплитудой 0.03 м и частотой 10 с^-1. Начальная фаза колебаний равна нулю. Определите: а)полную энергию шарика; б) отношение потенциальной энергии к кинетической для момента времени, когда шарик удален от положения равновесия на 0.02 м.

8. Точка, совершающая гармонические колебания, в некоторый момент времени имеет смещение 4·10^{-2 м}, скорость 0.05 м/с и ускорение 0.8 м/с². Определите: а) амплитуду, период колебаний; б) фазу колебаний в рассматриваемый момент времени; в) максимальные скорость и ускорение точки.

9. Амплитуда гармонических колебаний материальной точки А = 2 см, полная энергия колебаний Е = 0.30 мкДж. На каком смещении х от положения равновесия на колеблющуюся точку действует сила F = 22.5 мкН?

10. Найти отношение кинетической энергии точки, совершающей гармоническое колебание, к ее потенциальной энергии для моментов времени, когда смещение точки от положения равновесия составляет: х₁ = А/2, х₂ = А/4, х₃ = А. Начальная фаза колебаний j = 0. ( А – амплитуда колебаний).

11. Катушка с индуктивностью 30 мкГн присоединена к плоскому конденсатору с площадью пластин 10 см² каждая и расстоянием между ними 0.1 мм. Найти диэлектрическую проницаемость среды, заполняющей пространство между пластинами конденсатора, если контур резонирует на длину волны 750 м.

12. Дифференциальное уравнение колебаний заряда в контуре имеет вид: 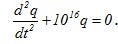. Индуктивность контура равна 10 мкГн. Найти емкость контура и записать уравнение колебаний заряда, если в начальный момент времени сила тока максимальна и равна 10 мА.

13. Уравнение изменения силы тока в колебательном контуре со временем дается в виде I(t) = – 0,02·sin(400pt), A. Индуктивность контура 1 Гн. Найти: 1) период колебаний; 2) емкость контура; 3) максимальное напряжение на конденсаторе; 4) максимальную энергию магнитного поля катушки индуктивности; 5) максимальную энергию электрического поля конденсатора.

14. Заряд конденсатора в колебательном контуре меняется по закону q=Acos(pt), где А = 2 мкКл. Найдите энергию электрического поля конденсатора в момент времени, когда она равна энергии магнитного поля катушки. Индуктивность катушки равна 0.05 Гн.

15. Колебательный контур состоит из из конденсатора емкостью 200 нФ и катушки индуктивностью 2 мГн. Чему равно максимальное напряжение на обкладках конденсатора, если максимальная сила тока равна 0.5 А? На какую длину волны настроен этот контур?

16. Заряд конденсатора в колебательном контуре меняется по закону q=Acos(pt), где А = 2 мкКл. Найдите энергию электрического поля конденсатора в момент времени, когда она равна энергии магнитного поля катушки. Индуктивность катушки равна 0.05 Гн.

17. В идеальном колебательном контуре заряд конденсатора меняется по закону q = q_maxcos(wt), где q_max = 5 мкКл, w = 10⁸  рад/c. Определить энергию электрического поля конденсатора в момент времени t₁ = T/8 (T – период колебаний в контуре).

18. Длина l электромагнитной волны в вакууме, на которую настроен колебательный контур, равна 12 м. Пренебрегая активным сопротивлением контура, определить максимальный заряд q_m на обкладках конденсатора, если максимальная сила тока в контуре I_m = 1 А.

19. В электрическом контуре, индуктивность которого равна 2×10^-7 Гн, происходят незатухающие электромагнитные колебания. Амплитуды заряда и силы тока в контуре равны, соответственно, 2×10^-8 Кл и 1А. Найдите емкость конденсатора и длину волны, на которую настроен контур.

20. Какую индуктивность надо включить в колебательный контур, чтобы при емкости 2.0 мкФ получить частоту собственных колебаний, равную 1000 Гц?

21. Складываются два гармонических колебания одинаковой частоты и одинакового направления: x₁ = A₁cos(wt + j₁), x₂ = A₂cos(wt + j₂), где А₁=1 см, j₁=p/3 рад; А₂=2 см, j₂ = 5p/6 рад. Определить амплитуду и начальную фазу j результирующего колебания. Запишите уравнение этого колебания.

22. Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых x = A₁cos(wt), y=A₂cos(wt/2), где A₁ = 1 см, A₂ = 2 см, w = p, рад/c. Найти уравнение траектории точки. Построить траекторию с соблюдением масштаба и указать направление движения точки.

23. Складываются два гармонических колебания одного направления, имеющие одинаковые амплитуды и одинаковые начальные фазы с периодами Т₁ = 2 с и Т₂ = 2.02 с. Определите период результирующего колебания и период биений.

24. Складываются два гармонических колебания одного направления с одинаковыми периодами: Т₁ = Т₂ = 1.5 с и амплитудами А₁ =А₂ = 2 см. Начальные фазы колебаний j₁ = p/2 рад и j₂ = p/3 рад. Определить амплитуду и начальную фазу j результирующего колебания. Запишите уравнение этого колебания.

25. Складываются два взаимно перпендикулярных колебания, выражаемых уравнениями: x = A₁sinwt, y = A₂cos(wt+t), где A₁ = 2 см, A₂=1 см, w=p с^-1, t = 0.5 с. Найти уравнение траектории y = y(x) и построить ее, указав направление движения точки.

26. В результате сложения двух колебаний, период одного из которых Т₁=0.02с, получают биения с периодом Т_б = 0.2 с. Определите период второго складываемого колебания.

27. Складываются два гармонических колебания одинаковой частоты и одинакового направления: x₁ = A₁cos(wt + j₁), x₂ = A₂cos(wt + j₂), где А₁=2 см, j₁=p/4 рад, А₂=1 см, j₂ = 3p/5 рад. Определить амплитуду и начальную фазу j результирующего колебания. Запишите уравнение этого колебания.

28. Амплитуда результирующего колебания, получающегося при сложении двух одинаково направленных гармонических колебаний одинаковой частоты, обладающих разностью фаз j = 60°, равна А = 6 см. Определите амплитуду А₂ второго колебания, если А₁ = 5 см.

29. Складываются два взаимно перпендикулярных колебания, выражаемых уравнениями: x = 2 cos(wt), y = -cos(2wt). Найти уравнение траектории y=y(x) и построить ее, указав направление движения точки.

30. Складываются три гармонических колебания одного направления с одинаковыми периодами Т₁ = Т₂ = Т₃ и амплитудами A₁ = A₂ = A₃ = 3 см. Начальные фазы колебаний j₁ = 0, j₂ = p/3, j₃ = p/3, рад. Используя метод векторных диаграмм, найти амплитуду и начальную фазу результирующего колебания. Записать уравнение этого колебания.

31. Найти логарифмический декремент затухания математического маятника, если за время t= 1 мин амплитуда колебаний уменьшилась в 2 раза. (Длина маятника l = 1 м).

32. Колебательный контур имеет индуктивность 0.01 Гн, емкость 4 мкФ и сопротивление 2 Ом. Определить логарифмический декремент затухания и добротность контура. Записать уравнение затухающих колебаний для заряда. Начальный заряд на пластинах конденсатора максимальный и равен 400 мКл.

33. Затухающие колебания точки происходят по закону 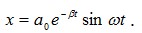. Найти: а) амплитуду смещения и скорость точки в момент времени  t = 0; б) моменты, когда точка достигает крайних положений.

34. В контуре, добротность которого равна 100 и собственная частота колебаний 50 кГц, возбуждаются затухающие колебания. Через сколько времени, энергия, запасенная в контуре, уменьшится в два раза? Определить коэффициент затухания.

35. Амплитуда затухающих колебаний математического маятника за 1 мин уменьшилась в 3 раза. Определите, во сколько раз она уменьшится за 4 мин.

36. Собственная частота колебаний контура n₀ = 8 кГц, добротность контура Q = 72. В контуре возбуждаются затухающие колебания. Найти закон убывания запасенной в контуре энергии W со временем, если в начальный момент времени энергия, запасенная в контуре равна 50 мкДж.

37. Тело массой m = 100 г, совершая затухающие колебания, за 2 мин потеряло 60% своей энергии. Определите коэффициент сопротивления среды.

38. Колебательный контур состоит из катушки индуктивностью L=10 мГн, конденсатора емкостью С=0.1 мкФ и резистора сопротивлением R=20 Ом. Определите, через сколько полных колебаний амплитуда тока в контуре уменьшится в e раз.

39. Логарифмический декремент затухания маятника l= 0.01. Определите число полных колебаний маятника до уменьшения амплитуды в 3 раза.

40. Собственная частота контура равна n₀ = 8,0 кГц; добротность контура Q=72. В контуре возбуждаются затухающие колебания. Найти закон убывания запасенной  в контуре энергии W со временем t. Какая часть первоначальной энергии W₀ сохранится в контуре по истечении промежутка времени t =1.00 мс?

41. Катушка с индуктивностью 30 мкГн присоединена к плоскому конденсатору с площадью пластин 10 см² каждая и расстоянием между ними 0.1мм. Найти диэлектрическую проницаемость среды, заполняющей пространство между пластинами конденсатора, если контур резонирует на длину волны 750 м.

42. Тело совершает вынужденные колебания в среде с коэффициентом затухания r = 1 г/с. Считая затухание малым, определите амплитудное значение вынуждающей силы, если резонансная амплитуда А_рез = 0.5 см, а частота собственных колебаний n₀ = 10 Гц.

43. В цепь переменного тока напряжением  U = 220 B включены последовательно емкость С, сопротивление R и индуктивность L. Найти падение напряжения  U_R  на сопротивлении, если известно, что падение напряжения на конденсаторе  U_C = 2U_R, на индуктивности  U_L = 3U_R.

44. Во сколько раз амплитуда вынужденных колебаний будет меньше резонансной амплитуды, если частота изменения вынуждающей силы будет больше резонансной частоты в два раза? Коэффициент затухания равен 0.1 w₀ (w₀ – циклическая частота свободных незатухающих колебаний).

45. Катушка с активным сопротивлением R=10 Ом и индуктивностью L включена в цепь переменного тока напряжением U = 7 B и частотой n=50 Гц. Найти индуктивность L катушки, если известно, что катушка поглощает мощность P = 400 Вт  и сдвиг фаз между напряжением и током j=60⁰.

46. Колебательная система совершает затухающие колебания с частотой n=1000 Гц. Определить собственную частоту колебаний n₀, если известно, что резонансная частота равна 998 Гц.

47. Какой должна быть добротность контура Q, чтобы частота, при которой наступает резонанс токов, отличалась от частоты , при которой наступает резонанс  напряжений, не более чем на 1 %?

48. Колебательный контур, подключенный к генератору, содержит резистор сопротивлением 5 Ом, катушку индуктивностью 5 Гн и конденсатор. Определите электроемкость конденсатора, при которой в контуре возникает резонанс при частоте 1 кГц. Чему равна сила тока в цепи при резонансе, если действующее напряжение на генераторе равно 220 В.

49. Период затухающих колебаний в системе равен Т = 0.2 с, а отношение амплитуд первого и шестого колебаний равно 13. Определить резонансную частоту данной колебательной системы.

50. Амплитуды вынужденных колебаний при частотах n₁=400 Гц и n₂=600 Гц равны между собой. Определить резонансную частоту n. Затуханием пренебречь.

51. Волна распространяется в упругой среде со скоростью 150 м/с. Определить частоту n колебаний, если минимальное расстояние Dx между точками среды, фазы колебаний которых противоположны, равно 0.75 м.

52. В однородной среде распространяется плоская упругая волна вида  , где a, b, w  и k – постоянные. Найти разность фаз колебаний в точках, где амплитуды смещения частиц среды отличаются друг от друга на  h = 1 %, если  b = 0.42 м^-1  и длина волны  l = 50  см.

53. Плоская монохроматическая волна распространяется вдоль прямой, совпадающей с положительным направлением оси 0x в среде, не поглощающей энергию, со скоростью v = 15 м/с. Две точки, находящиеся на этой прямой на расстояниях x₁ = 5 м и x₂ = 5,5 м от источника колебаний, колеблются с разностью фаз Dj = p/5. Амплитуда волны A = 0,04 м. Определить: 1) длину волны l, 2) уравнение волны, 3) смещение s₁ первой точки в момент времени t₁ = 3 с.

54. Смещение от положения равновесия точки, отстоящей от источника колебаний на расстоянии l = 4 см, в момент времени t = T/6 (Т – период колебаний) равно половине амплитуды. Найти длину бегущей волны.

55. Поперечная волна распространяется вдоль упругого шнура со скоростью v=15 м/с. Период колебаний точек шнура равен Т = 1.2 с, амплитуда A=2 см. Определить: 1) длину волны; 2) фазу колебаний, смещение , скорость и ускорение точки, отстоящей на расстоянии х = 45 м от источника волн в момент t=4 с; 3) разность фаз колебаний двух точек, лежащих на луче и отстоящих от источника волн на расстояниях x₁ = 20 м и x₂ = 30 м.

56. На расстоянии l=4 м от источника плоской волны частотой v = 440 Гц перпендикулярно ее лучу расположена стена. Определить расстояния от источника волн до точек, в которых будут первые три узла и три пучности стоячей волны, возникшей в результате сложения бегущей и отраженной от стены волн. Скорость волны считать равной 440 м/с.

57. Уравнение бегущей плоской упругой волны имеет вид ξ = 60cos(1800t-5.3x), где x в микрометрах, t - в секундах, х - в метрах. Найти: а) отношение амплитуды смещения частиц среды к длине волны; б) амплитуду колебаний скорости частиц среды и ее отношение к скорости распространения волны.

58. Поплавок на волнах за время t = 20 с совершил N₁ = 30 колебаний, при этом на отрезке l = 20 м, перпендикулярном к направлению распространения волны наблюдатель насчитал N₂ = 10 гребней. Найдите скорость распространения волны.

59. Найти смещение х от положения равновесия точки, отстоящей на источника колебаний на расстоянии l = l/2, для момента времени t = T/6 (Т – период колебаний). Амплитуда колебаний А = 0.05 м.

60. Смещение от положения равновесия точки, отстоящей от источника колебаний на расстоянии l = 4 см, в момент времени t = T/6 равно половине амплитуды. Найти длину бегущей волны.

61. Два звуковых сигнала частотой 40 Гц, синхронно излучаемые из двух различных точек, находящихся на одинаковом расстоянии l = 550 м от точки А на берегу озера. Один сигнал приходит от источника В, находящегося в воде, другой идет от источника С, расположенного в воздухе. Выясните, будут ли эти сигналы усиливать или ослаблять друг друга. Скорость звука в воде 1500 м/с, в воздухе – 340 м/с.

62. Определите длину звуковой волны l в воде, вызываемой источником колебаний с частотой n = 250 Гц, если скорость звука в воде равна 1450 м.

63. Летучая мышь приближается перпендикулярно к стене со скоростью 6м/с, издавая ультразвук частотой 45 кГц. Какие две частоты звука n₁ и n₂ слышит летучая мышь? Скорость звука в воздухе считать равной 340 м/с.

64. Человеческое ухо может воспринимать звуки частотой приблизительно от n₁ = 20 Гц до n₂ = 20 кГц. Между какими длинами волн лежит интервал слышимости звуковых колебаний?

65. Зная, что средняя квадратичная скорость молекул двухатомного газа в условиях опыта равна 461 м/c, найти скорость распространения звука в газе.

66. Два поезда идут навстречу друг другу со скоростями V₁ = 72 км/ч и V₂ = 54 км/ч. Первый поезд дает свисток с частотой n = 600 Гц. Найти частоту колебаний звука, которую слышит пассажир второго поезда перед встречей поездов. Скорость распространения звука в воздухе V_зв = 340 м/с.

67.  Шум на улице громкостью 80 фон слышен в квартире, как шум громкостью 40 фон. Определите отношение интенсивностей этих звуков.

68. Расстояние между двумя соседними пучностями стоячей волны, создаваемой камертоном с частотой 450 Гц в воздухе, составляет 36.9 см. Определите скорость звука в воздухе.

69. Когда поезд проходит мимо неподвижного наблюдателя, частота тона гудка паровоза меняется скачком. Какой процент от истинной частоты тона составляет скачок частоты, если поезд движется со скоростью V = 60 км/ч?

70. Найти скорость распространения звука в двухатомном газе, если известно, что при давлении р = 1.01∙10⁵ Па плотность газа равна r = 1.29 кг/м³.

71. Радиолокатор обнаружил в море подводную лодку, отраженный сигнал от которой дошел до него за 36 мкс. Считая, что диэлектрическая проницаемость воды равна 81, определить расстояние от локатора до подводной лодки.

72. Уравнение электромагнитной волны, распространяющейся в керосине, дано в виде: E = 200 cos (2×10⁸t – 1.3), В/м. Определить длину волны в воздухе и скорость ее распространения в керосине.

73. Импульс, переносимый плоской электромагнитной волной в вакууме через площадку S = 10 см² за τ = 5.0 с, равен p = 10^{-2 кг м/с}. Найти интенсивность I волны.

74. Электромагнитная волна с частотой ν = 3.0 МГц переходит из вакуума в немагнитную среду с диэлектрической проницаемостью ε = 4.0. Найти приращение ее длины волны.

75. В однородной среде с ε=4 и μ=1 распространяется плоская электромагнитная волна с амплитудой напряженности электрического поля E_m=200 В/м. Найти для этой волны: а) амплитуду магнитной индукции B_m; б) скорость распространения волны v; в) амплитуду вектора Умова - Пойнтинга S_m.

76. Найти скорость v распространения электромагнитных волн в кабеле, в котором пространство между внешним и внутренним проводом заполнено диэлектриком с диэлектрической проницаемостью ε =4.5. Потерями в кабеле пренебречь.

77. Плоская гармоническая электромагнитная волна в немагнитной среде (μ=4,0) имеет следующие параметры: E_m = 5,0∙10^-5 В/м; λ=100 м; ν=1 МГц. Какая энергия W переносится волной за время τ =10 мин через площадку S=1.0 м², расположенную перпендикулярно скорости распространения волны?

78. В вакууме распространяется плоская электромагнитная волна, амплитуда напряженности магнитного поля которой Н₀ = 0.05 А/м. Определите: а) амплитуду напряженности электрического поля волны; б) среднюю объемную плотность энергии; в) интенсивность волны.

79. На расстоянии 5 м от источника в момент времени t = T/6 значение напряженности электрического поля плоской электромагнитной волны в два раза меньше амплитудного значения. Определите длину волны, если в начальный момент времени напряженность электрического поля в месте расположения источника равна нулю.

80. В вакууме вдоль оси х распространяется плоская электромагнитная волна. Определите амплитуду напряженности магнитного поля волны, если амплитуда напряженности электрического поля волны равна 5 В/м.

Автор страницы: Лев Васильев