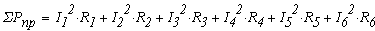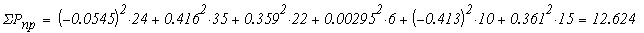Линейные цепи постоянного тока

Контрольная работа №1

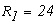
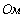
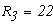
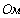
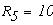
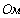
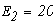
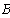
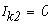
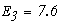
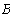
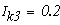
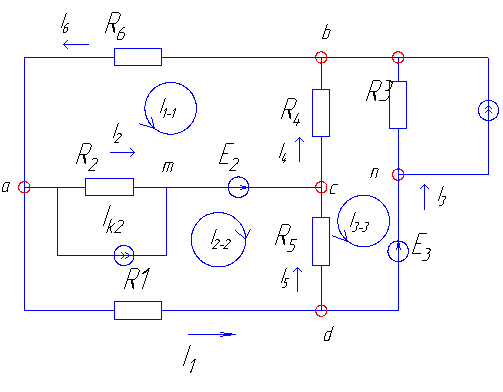
1.1 Уравнения по законам Кирхгофа.

1. Намечаем произвольно направления токов во всех ветвях (см схему)

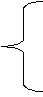
2. Составляем уравнения по первому закону Кирхгофа. Для нашей схемы с четырьмя узлами нужно составить три уравнения

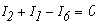
- для узла А

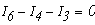
- для узла В

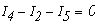
- для узла С

3. выбираем произвольно направление обхода каждого контура цепи и составляем уравнения по второму закону Кирхгофа. Контуры, для которых составляются уравнения, нужно выбрать так, чтобы каждый из них включал в себя хотя бы одну ветвь не вошедшую в другие контуры. Только при этом условии уравнения, составленые по второму закону Кирхгофа, будут независимыми друг от друга. Поэтому и контуры, выбранные с соблюдением приведенного выше условия , принято называть независимыми. Таким образом, число уравнений, составленых по второму закону Кирхгофа должно быть равно числу независимых контуров:

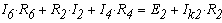
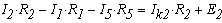
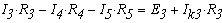
В этих уравнениях все ЭДС и токи, совпадающие с направлением обхода, записываются со знаком "+" , нправленные навстречк обходу - со знаком "-" . Как видно из данного примера, общее число уравнений, составленных по первому и второму законам кирхгофа равно числу неизвестных токов, т.е. числу ветвей.

Решив эту систему уравнений с шестью неизвестными, определим искомые токи. Если какой либо ток получился отрицательным, то это означает, что его действительное направление противоположно направлению выбранному в п.1.

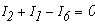
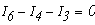
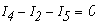
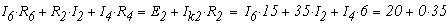
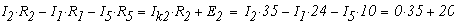
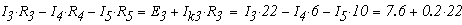
Решая эту систему уравнений получим токи:

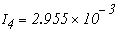
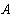
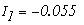
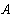
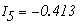
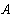
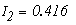
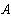
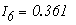
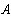
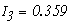
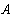
Рассмотреный метод расчета в подавляющем большинстве случаев является достаточно громоздким и потому практически нецелесообразным. Задача практически упрощается при использовании метода контурных токов и метода узловых потенциалов, в основу которых положены уравнения Кирхгофа.

1.2 Метод контурных токов.

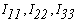
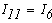
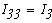
1.Вводим понятие фиктивных контурных токов: и выбераем произвольно направление каждого из них. Значения контурных токов должны быть равны по абсолютной величине значениям токов в несмежных ветвях, т.е.

Тогда токи во всех ветвях схемы определяются из выражений(1)

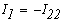
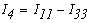
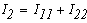
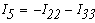
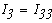
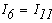
Таким образом, при использовании методом контурных токов уравнения, составвленные по первому закону Кирхгофа, обращаются в тождества, т.е. этот закон удовлетворяет при любых значениях контурных токов. Значит для решения задачи этим методом достаточно уравнений, составленых по 2-му закону Кирхгофа.

2. Составляем уравнение по 2-му закону Кирхгофа для контурных токов. Для этого подставим в первое из уравнений значения токов в ветвях приведенное в уравнениях (3)

Подставив числовые данные ЭДС и сопротивлений получим:

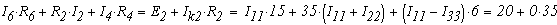
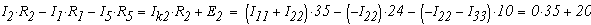
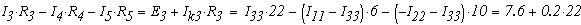
Получим

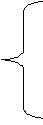
Δ =

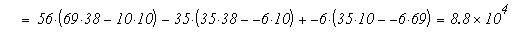
Так как Δ не равен 0, то система имеет единственное решение. Вычислим вспомогательные определители

=

=

=

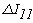
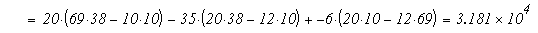
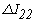
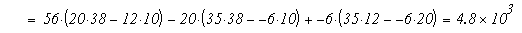
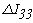
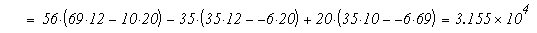
Воспользовавшись формулами Крамера, получим

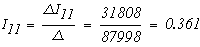
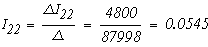
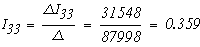
Значения токов в ветвях определяется из выражения

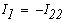
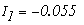
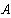
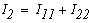
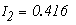
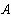
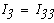
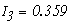
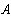
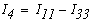
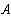
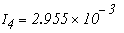
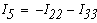
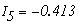
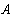
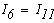
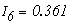
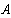
Метод узловых потенциалов

При известных потенциалов отдельных узолов ток в каждой ветви можно определить по закону Ома:

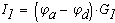
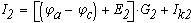
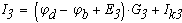
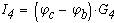
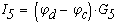
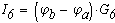
Из этих соотношений видно, что токи в ветвях зависят от разностей потенциалов узлов, к которым ветви присоединены. Это позволяет задать потенциалу одного из узлов любое числовое значение.

Порядок расчета рассматриваемой цепи следующий.

Полагаем потенциал узла схемы (нпример узел а) равен нулю:

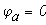
Для всех остальных узлов составляем уравнения по первому закону Кирхгофа, выразив значения токов из верхней системы уравнений. В этом случае уравнение из узла а примет вид:

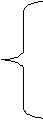
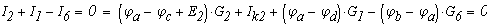
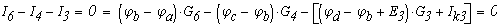
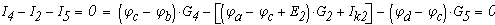
Определим численные значения проводимостей и подставим их в последнюю систему уравнений:

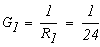
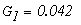
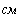
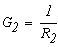
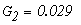
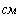
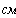
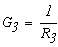
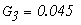
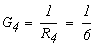
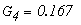
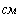
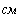
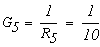
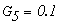
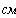
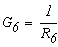
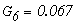
тогда

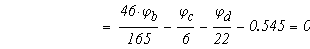
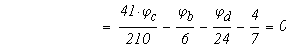
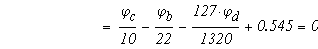
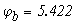
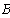
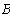
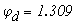
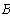
Определяем токи в ветвях

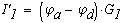
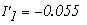
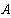
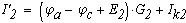
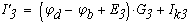
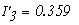
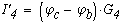
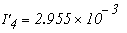
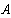
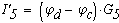
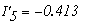
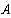
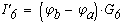
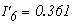
Как видно значения токов при методе контурных токов и при методе узловых потенциалов не отличаются.

1.4 Метод активного двухполюсника.

Этот метод применяется для определения тока в одной ветви.

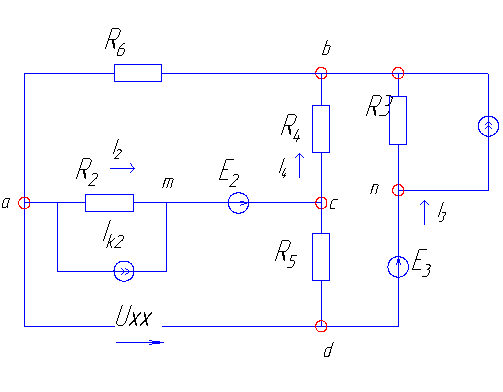
1. Разрываем ветвь, ток в которой нужно определить, и подсчитываем напряжение между точками разрыва (напряжение холостого хода). Полученная схема изображена на рисунке.

Для нахождения 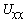найдем токи в ветвях этой схемы методом контурных токов.

для этого выберем произвольно направления токов в ветвях схемы и направления контурных токов

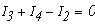
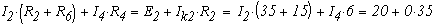
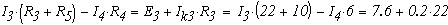
Получим токи:

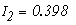
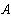
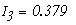
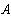
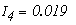
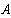
Определим напряжение холостого хода

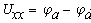
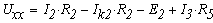
При известных величинах получаем:

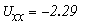
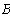
Внутренне сопротивление эквивалентного источника равно входному сопротивлению относительном выводов пассивного двухполюсника.

Входное сопротивление двухполюсника относительно наружных выводов определяется при устранении из схемы активного двухполюсника всех источников.

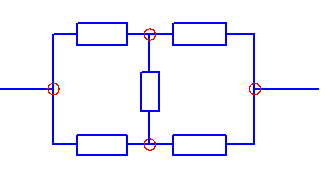
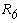
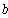
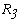
Перерисуем данную схему заменив соединение треугольником на эквивалентное сопротивление звездой.

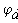
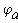
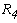
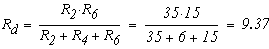
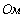
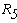
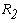
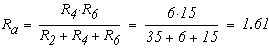
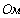
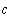
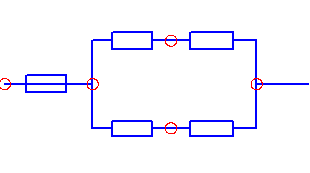
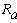
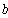
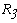
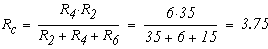
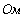
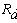
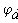
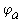
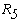
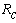
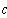
Тогда

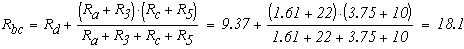
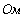
Внетреннее сопротивление эквивалентного источника

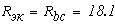
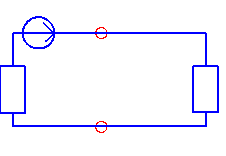
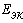
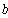
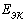
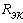
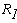
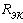
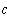
Окончательная расчетная схема имеет вид одноконурной цепи, включающей эквивалентный источник с ЭДС и внутренним сопротивлением заменяющим активный двухполюсник

тогда по закону Ома:

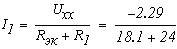
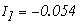
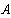
Видно, что полученное значение хорошо совпадает со значением тока, полученным ранее.

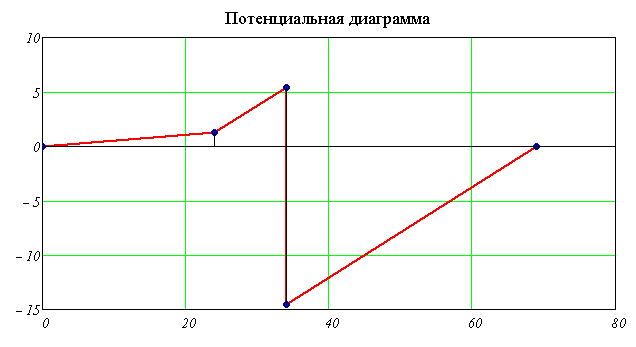
1.5 Потенциальная диаграмма.

Потенциальная диаграмма представляет собой график изменения потенциала вдоль амкнутого контура.

Отложим по оси абцисс все сопротивления контура. двигаяс от точки а, потенциал которой равен нулю. Перемещаясь вдоль этого контура, подсчитываем потенциалы этих точек.

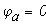
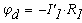
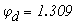
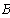
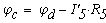
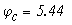
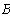
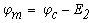
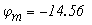
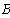
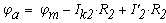
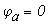
Значения найденных потенциалов с достаточной точностью совпадают с найденными по методу узловых потенциалов

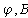
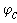
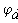
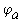
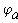
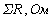
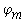
1.6 Баланс мощностей

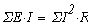
Мощность, генерируемая источниками

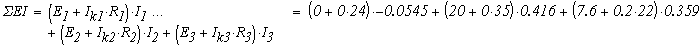
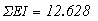
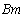
Суммарная мощность приемников