Теоретическая механика ИжГСХА (статика, кинематика)
<в начало
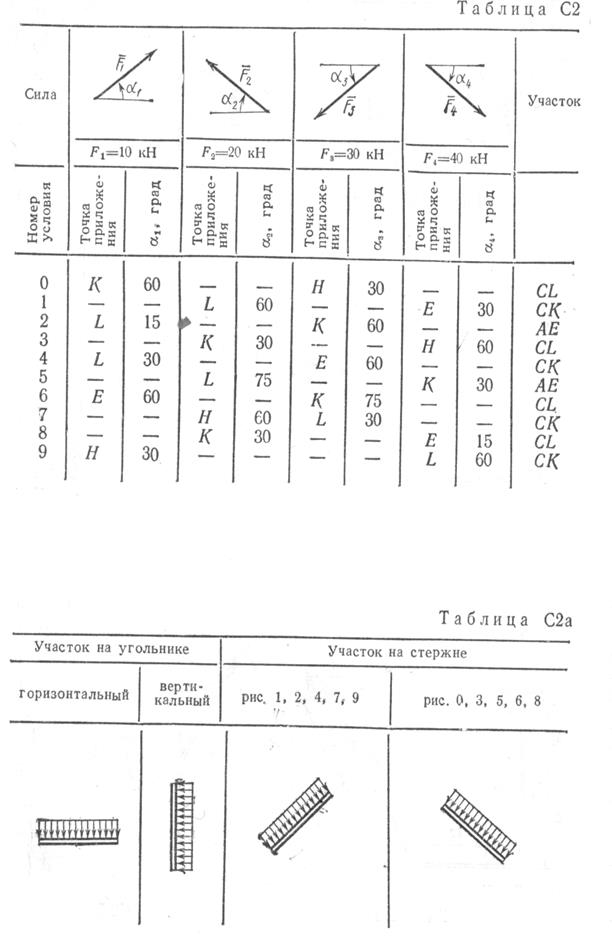
Статика С-1
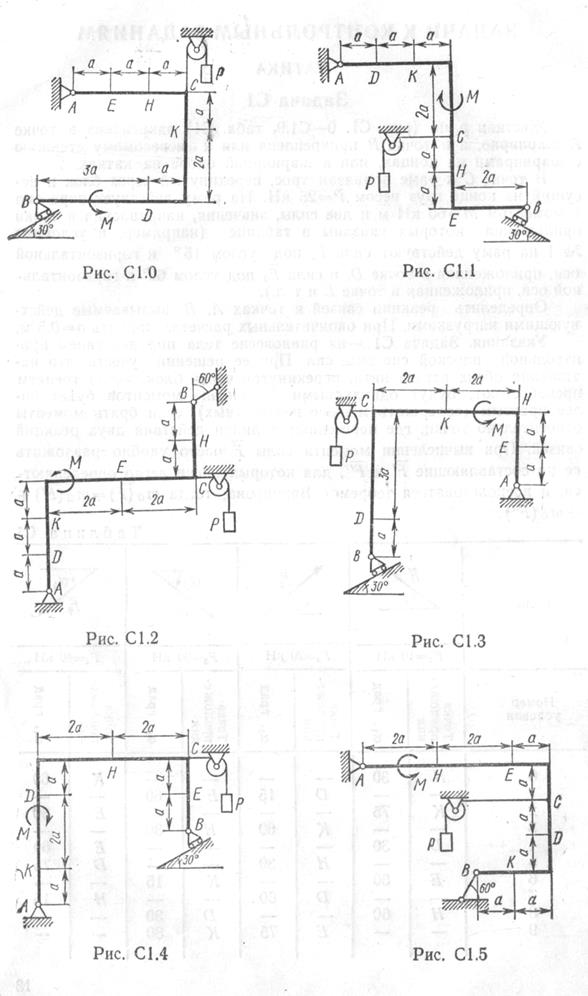
Жесткая рама массой 1000 кг закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню с шарнирами на концах, или к шарнирной опоре на катках.
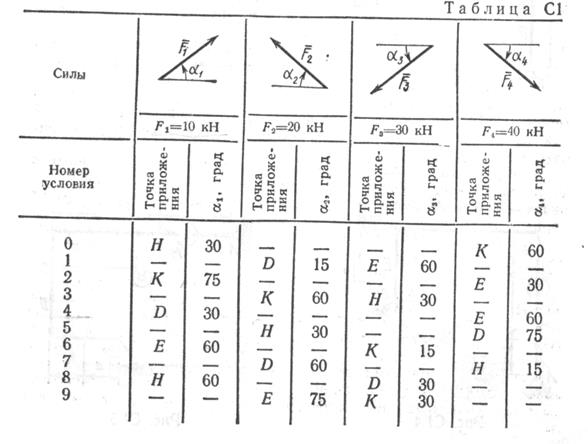
В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом 25 кН. На раму действует пара сил с моментом М = 60 кН м и две силы, значения которых указаны в таблице.
Определить реакции связей в точках А, В, вызываемые действующими нагрузками. При окончательных расчетах принять а = 0,5 м. См. условие задачи>
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 | Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант 10 |
| Вариант 11 | Вариант 12 | Вариант 13 | Вариант 14 | Вариант 15 | Вариант 16 | Вариант 17 | Вариант 18 | Вариант 19 | Вариант 20 |
| Вариант 21 | Вариант 22 | Вариант 23 | Вариант 24 | Вариант 25 | Вариант 26 | Вариант 27 | Вариант 28 | Вариант 29 | Вариант 30 |
| Вариант 31 | Вариант 32 | Вариант 33 | Вариант 34 | Вариант 35 | Вариант 36 | Вариант 37 | Вариант 38 | Вариант 39 | Вариант 40 |
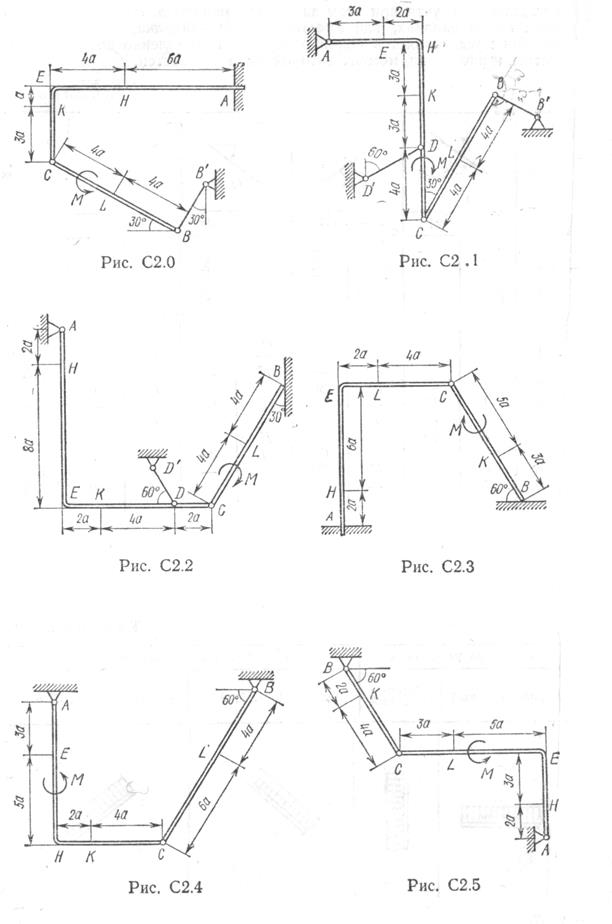
Статика С-2
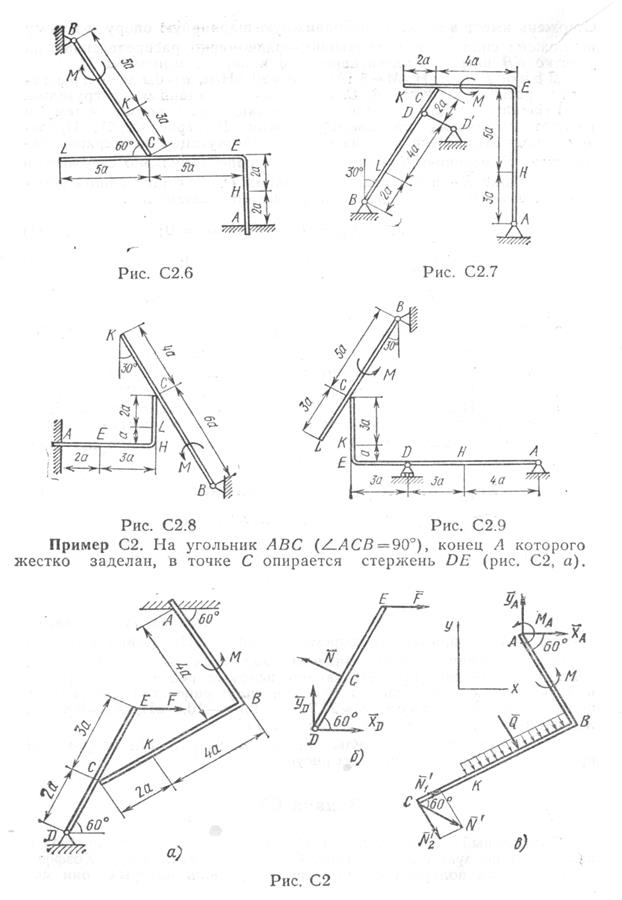
Конструкция состоит из жесткого угольника и стержня, которые в точке С или соединены друг с другом шарнирно или свободно опираются друг о друга. На конструкцию действует пара сил с моментом М = 60 кН м, распределенная нагрузка интенсивности q = 20 кН/м и две силы, значения которых , точки приложения и направления имеются в таблице; в этой же таблице в столбце «Участок» указано, на каком участке действует распределенная нагрузка. См. условие задачи>
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 | Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант 10 |
| Вариант 11 | Вариант 12 | Вариант 13 | Вариант 14 | Вариант 15 | Вариант 16 | Вариант 17 | Вариант 18 | Вариант 19 | Вариант 20 |
| Вариант 21 | Вариант 22 | Вариант 23 | Вариант 24 | Вариант 25 | Вариант 26 | Вариант 27 | Вариант 28 | Вариант 29 | Вариант 30 |
| Вариант 31 | Вариант 32 | Вариант 33 | Вариант 34 | Вариант 35 | Вариант 36 | Вариант 37 | Вариант 38 | Вариант 39 | Вариант 40 |
Кинематика К-1
Механизм состоит из ступенчатых колес 1 -3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 - r1=2см, R1=4см, у колеса 2 - r2=6см, R2=8см, у колеса 3 - r3=12см, R3=16см. На ободьях колес расположены точки А,В,С. См. условие задачи>
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 | Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант 10 |
| Вариант 11 | Вариант 12 | Вариант 13 | Вариант 14 | Вариант 15 | Вариант 16 | Вариант 17 | Вариант 18 | Вариант 19 | Вариант 20 |
| Вариант 21 | Вариант 22 | Вариант 23 | Вариант 24 | Вариант 25 | Вариант 26 | Вариант 27 | Вариант 28 | Вариант 29 | Вариант 30 |
| Вариант 31 | Вариант 32 | Вариант 33 | Вариант 34 | Вариант 35 | Вариант 36 | Вариант 37 | Вариант 38 | Вариант 39 | Вариант 40 |
Кинематика К-2
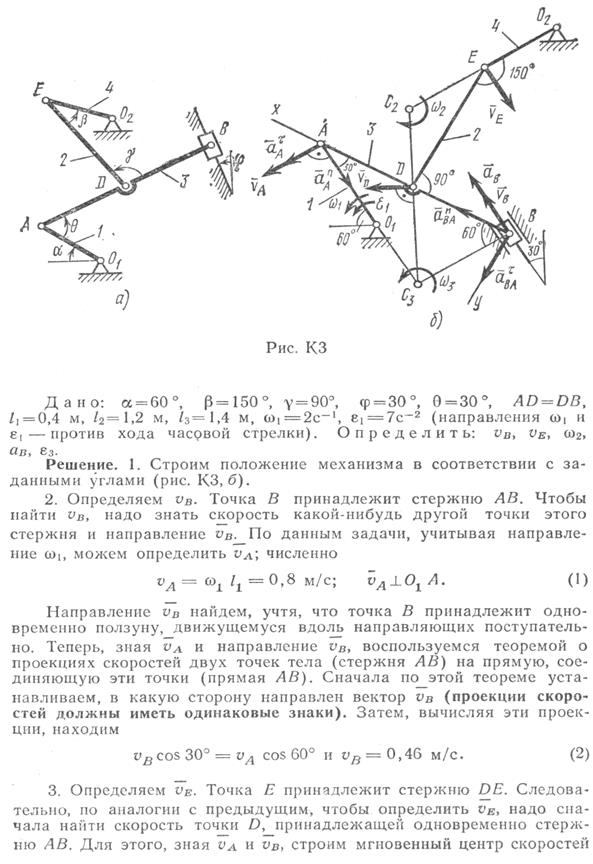
Плоский механизм состоит из стержней 1,2,3,4, и ползуна В или Е. Точка D находится в середине стержня АВ. Длины стержней соответственно равны: l1=0.4м, l2=1.2м, l3=1.4м, l4=0.6м. Положение механизма определяется углами 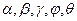 . Значения этих углов и других заданных величин указаны в таблице К2а или в таблице К2б, при этом в указанных таблицах
. Значения этих углов и других заданных величин указаны в таблице К2а или в таблице К2б, при этом в указанных таблицах 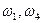 - величины постоянные. См. условие задачи>
- величины постоянные. См. условие задачи>
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 | Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант 10 |
| Вариант 11 | Вариант 12 | Вариант 13 | Вариант 14 | Вариант 15 | Вариант 16 | Вариант 17 | Вариант 18 | Вариант 19 | Вариант 20 |
| Вариант 21 | Вариант 22 | Вариант 23 | Вариант 24 | Вариант 25 | Вариант 26 | Вариант 27 | Вариант 28 | Вариант 29 | Вариант 30 |
| Вариант 31 | Вариант 32 | Вариант 33 | Вариант 34 | Вариант 35 | Вариант 36 | Вариант 37 | Вариант 38 | Вариант 39 | Вариант 40 |
Кинематика К-3
Прямоугольная пластина (рис.К3.0-К3.4) или круглая пластина радиуса R=60 см (рис.К3.5-К3.9) вращается вокруг неподвижной оси по закону , заданному в таблице К3. Положительное направление отчета углов показано на рисунках дуговой стрелкой. На рис. 0,1,2,5,6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 3,4,7,8,9 ось вращения лежит в плоскости пластины (пластина вращается в пространстве). См. условие задачи>
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 | Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант 10 |
| Вариант 11 | Вариант 12 | Вариант 13 | Вариант 14 | Вариант 15 | Вариант 16 | Вариант 17 | Вариант 18 | Вариант 19 | Вариант 20 |
| Вариант 21 | Вариант 22 | Вариант 23 | Вариант 24 | Вариант 25 | Вариант 26 | Вариант 27 | Вариант 28 | Вариант 29 | Вариант 30 |
| Вариант 31 | Вариант 32 | Вариант 33 | Вариант 34 | Вариант 35 | Вариант 36 | Вариант 37 | Вариант 38 | Вариант 39 | Вариант 40 |
Статика
Жесткая рама массой 1000 кг закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню с шарнирами на концах, или к шарнирной опоре на катках.
В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом 25 кН. На раму действует пара сил с моментом М = 60 кН м и две силы, значения которых указаны в таблице.
Определить реакции связей в точках А, В, вызываемые действующими нагрузками. При окончательных расчетах принять а = 0,5 м.
Указания. Задача С1 – на равновесие тела под действием произвольной плоской системы сил. При ее решении учесть, что натяжение обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковы. Силу тяжести рамы приложить к ее центру тяжести, положение центра тяжести определить. Чтобы уравнение моментов было более простым, нужно брать моменты относительно точки, в которой пересекаются линии действия двух реакций связей. При вычислении моментов силы, не параллельные выбранным координатным осям, удобно разложить на составляющие

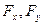
, для которых плечи легко определяются.
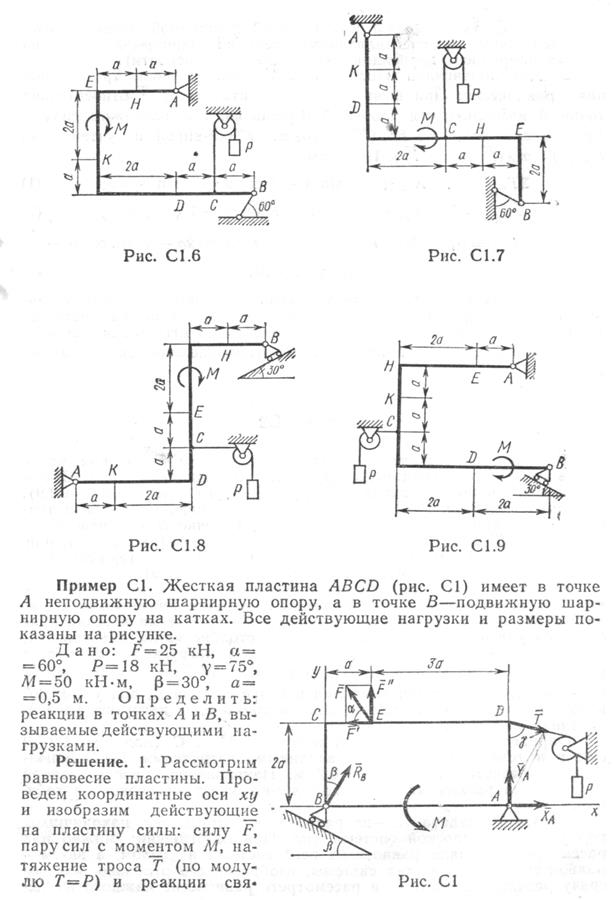

Конструкция состоит из жесткого угольника и стержня, которые в точке С или соединены друг с другом шарнирно или свободно опираются друг о друга. На конструкцию действует пара сил с моментом М = 60 кН м, распределенная нагрузка интенсивности q = 20 кН/м и две силы, значения которых , точки приложения и направления имеются в таблице; в этой же таблице в столбце «Участок» указано, на каком участке действует распределенная нагрузка.
Определить реакции связей в точках А,В,С ( для рис. 1,2,7,9 еще и в точке D ), вызванные данными нагрузками. При окончательных расчетах принять а = 0,2 м.
Указания. Задача С2 – на равновесие системы тел, находящихся под действием плоской системы сил. При ее решении следует расчленить систему и рассмотреть равновесие каждого из тел в отдельности, учтя при этом закон о равенстве действия и противодействия.

Механизм состоит из ступенчатых колес 1 -3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 -
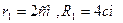
, у колеса 2 -
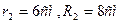
, у колеса 3 -
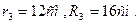
На ободьях колес расположены точки А,В,С.
В столбце «Дано» таблицы указан закон движения или закон изменения скорости ведущего звена механизма, где
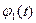
- закон вращения колеса 1,
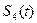
- закон движения рейки 4,
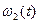
- закон изменения угловой скорости колеса 2,
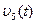
- закон изменения скорости груза 5 и т.д. (везде
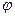
выражено в радианах,
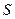
- в сантиметрах,
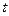
- в секундах). Положительное направление для
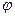
и
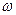
- против часовой стрелки, для
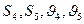
- вниз.
Определить в момент времени
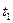
= 1 с указанные в таблице в столбцах «Найти» скорости и ускорения соответствующих точек или тел. Вектора скоростей и ускорений указанных точек или тел изобразить на чертеже, также указать на чертеже круговые стрелки, соответствующие векторам угловых скоростей и угловых ускорений тел, которым принадлежат указанные точки.
Указания. Задача К1 – на исследование простейших движений твердого тела. При решении задачи учесть, что при зацеплении колес скорости точек зацепления одинаковы, а при ременной передаче скорости всех точек ремня и, следовательно, точек, лежащих на ободе этих колес одинаковы при отсутствии проскальзывания и растяжения ремня.
Таблица К1

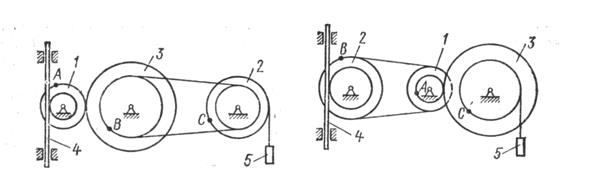
Рис. К1.0 Рис. К1.1
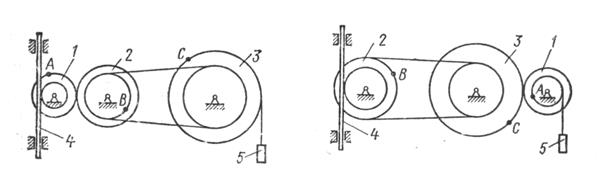
Рис. К1.2 Рис. К1.3
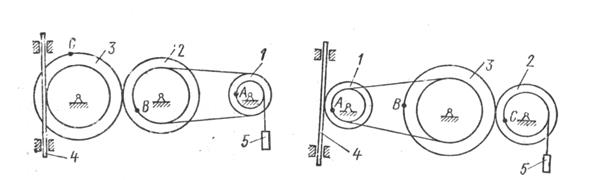
Рис. К1.4 Рис. К1.5
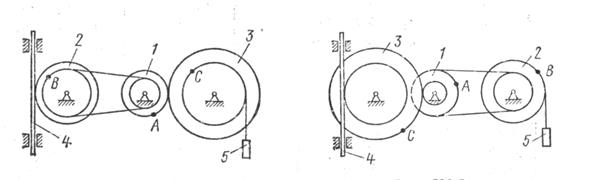
Рис. К1.6 Рис. К1.7
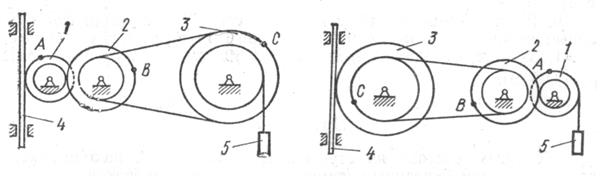
Рис. К1.8 Рис. К1.9
Пример К1. Рейка 1, ступенчатое колесо 2 с радиусами
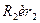
и колесо 3 радиуса
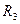
, скрепленное с валом радиуса
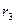
находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис. К.2). Рейка движется по закону
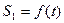
.

Плоский механизм состоит из стержней 1,2,3,4, и ползуна В или Е. Точка D находится в середине стержня АВ. Длины стержней соответственно равны:
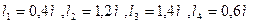
. Положение механизма определяется углами
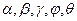
. Значения этих углов и других заданных величин указаны в таблице К2а или в таблице К2б, при этом в указанных таблицах
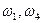
- величины постоянные.
Определить величины, указанные в таблицах в столбцах «Найти». Причем скорости указанных точек определить двумя способами: графоаналитическим, как показано в примере, и аналитическим.
Построение чертежа начинать со стержня, направление которого определяется углом
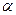
; ползун с направляющими для большей наглядности изобразить так, как в примере К2 (см. рис. К2б).
Заданные угловую скорость и угловое ускорение считать направленными против хода часовой стрелки, а заданные скорости
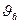
и ускорение
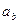
от точки В к b.
Указания. Задача К2 – на исследование плоскопараллельного движения твердого тела. При ее решении воспользоваться теоремами о скоростях и ускорениях точек плоской фигуры, а также понятием о мгновенном центре скоростей.
Таблица К2а (к рис. К2.0-К2.4)
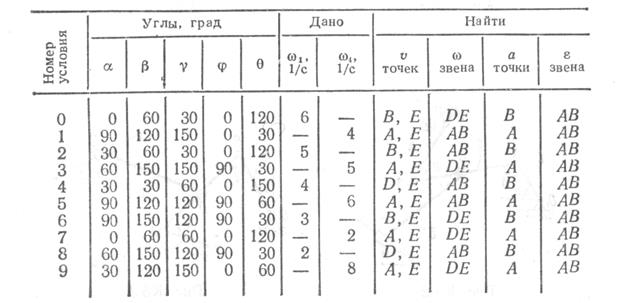
Таблица К2б (к рис. К2.5-К2.9)
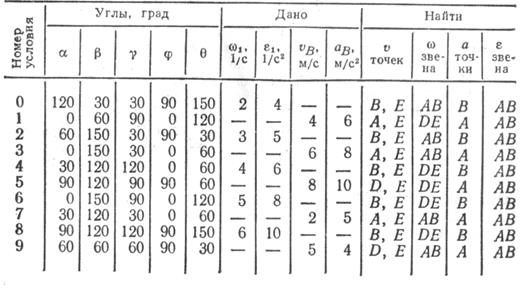
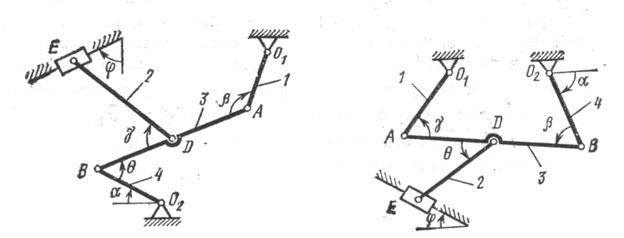
Рис. К2.0 Рис.К2.1
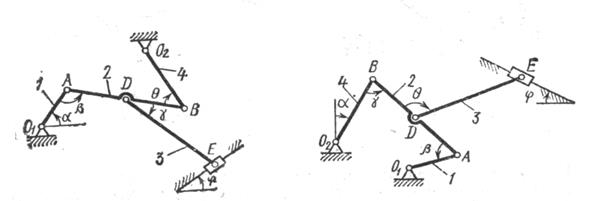
Рис.К2.2 Рис.К2.3
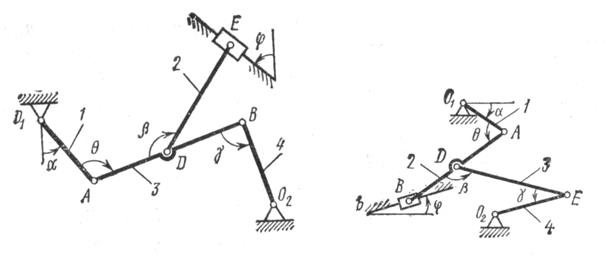
Рис.К2.4 Рис.К2.5
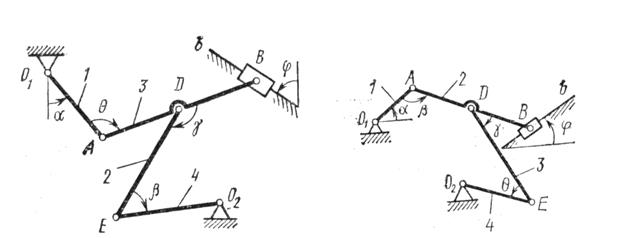
Рис.К2.6 Рис.К2.7
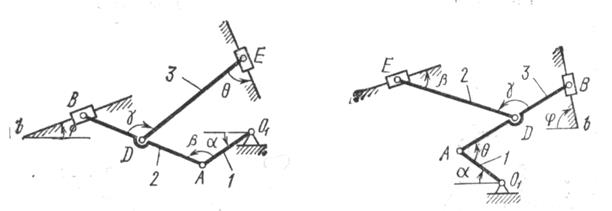
Рис.К2.8 Рис.К2.9
Пример К2. Механизм (рис.К2.а) состоит из стержней 1,2,3,4 и ползуна В, соединенных друг с другом и с неподвижными опорами
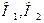
шарнирами.


Прямоугольная пластина (рис.К3.0-К3.4) или круглая пластина радиуса R=60 см (рис.К3.5-К3.9) вращается вокруг неподвижной оси по закону
, заданному в таблице К3. Положительное направление отчета углов
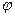
показано на рисунках дуговой стрелкой. На рис. 0,1,2,5,6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 3,4,7,8,9 ось вращения
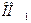
лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой ВD (рис. 0-4) или по окружности радиуса R (рис. 5-9) движется точка М; закон ее относительного движения, т.е. зависимость
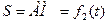
(
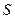
выражено в сантиметрах, t – в секундах), задан в таблице отдельно для рис.0-4 и для рис.5-9; там же даны размеры b и
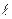
. На рисунках точка М показана в положении, при котором
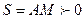
(при
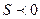
точка М находится по другую сторону от точки А).
Найти абсолютную скорость и абсолютное ускорение точки М в момент времени
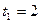
с.
Указания. Задача К3 – на сложное движение точки. Для ее решения воспользоваться теоремами о сложении скоростей и сложении ускорений при сложном движении точки. Прежде чем проводить расчеты, следует по условию задачи определить, где находится точка М на пластине в момент времени
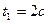
, и изобразить точку именно в этом положении (а не в произвольном, как показано на рисунках к задаче)
В случаях, относящихся к рис. 5-9, при решении задачи не подставлять числового значения R, пока не будут определены положения точки М в момент времени
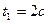
и угол между радиусами СМ и СА в этот момент.
Таблица К3
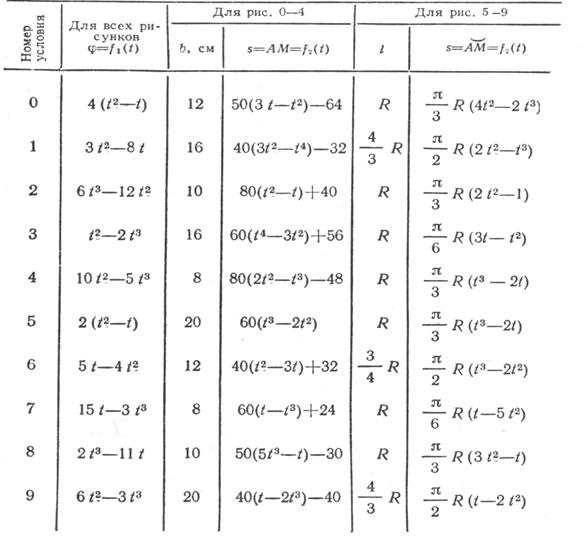
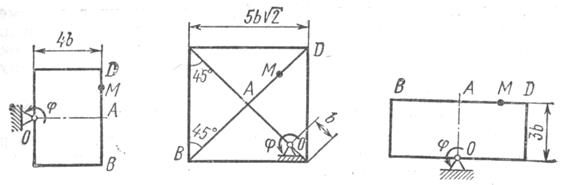
Рис. К3.0 Рис.К3.1 Рис. К3.2
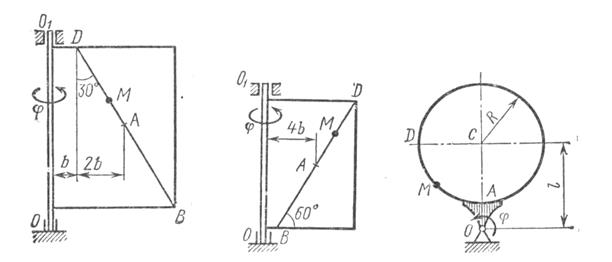
Рис. К3.3 Рис.К3.4 Рис. К3.5
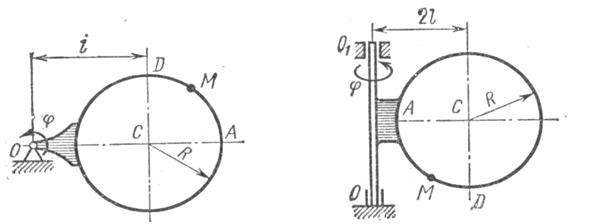
Рис.К3.6 Рис.К3.7
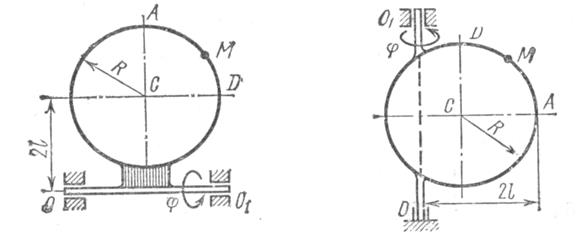
Рис.К3.8 Рис.К3.9
Пример К3 Шар радиуса R (рис К3.а) вращается вокруг своего диаметра АВ по закону
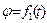
. По дуге большого круга («меридиану») АДВ движется точка М по закону
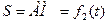
.

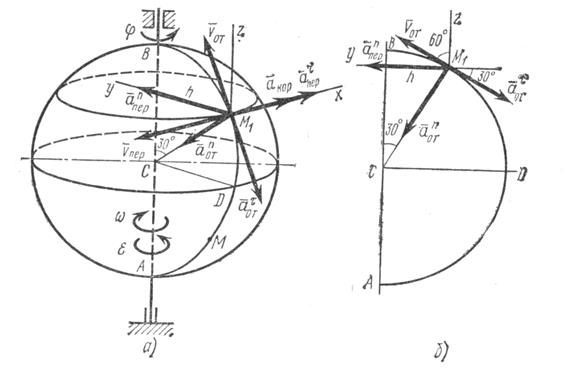
Рис. К3


Статика
Задача С1
Жесткая рама массой 1000 кг закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню с шарнирами на концах, или к шарнирной опоре на катках.
В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом 25 кН. На раму действует пара сил с моментом М = 60 кН м и две силы, значения которых указаны в таблице.
Определить реакции связей в точках А, В, вызываемые действующими нагрузками. При окончательных расчетах принять а = 0,5 м.
Указания. Задача С1 – на равновесие тела под действием произвольной плоской системы сил. При ее решении учесть, что натяжение обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковы. Силу тяжести рамы приложить к ее центру тяжести, положение центра тяжести определить. Чтобы уравнение моментов было более простым, нужно брать моменты относительно точки, в которой пересекаются линии действия двух реакций связей. При вычислении моментов силы, не параллельные выбранным координатным осям, удобно разложить на составляющие ![]()
![]() , для которых плечи легко определяются.
, для которых плечи легко определяются.




Задача С2
Конструкция состоит из жесткого угольника и стержня, которые в точке С или соединены друг с другом шарнирно или свободно опираются друг о друга. На конструкцию действует пара сил с моментом М = 60 кН м, распределенная нагрузка интенсивности q = 20 кН/м и две силы, значения которых , точки приложения и направления имеются в таблице; в этой же таблице в столбце «Участок» указано, на каком участке действует распределенная нагрузка.
Определить реакции связей в точках А,В,С ( для рис. 1,2,7,9 еще и в точке D ), вызванные данными нагрузками. При окончательных расчетах принять а = 0,2 м.
Указания. Задача С2 – на равновесие системы тел, находящихся под действием плоской системы сил. При ее решении следует расчленить систему и рассмотреть равновесие каждого из тел в отдельности, учтя при этом закон о равенстве действия и противодействия.




Задача К1
Механизм состоит из ступенчатых колес 1 -3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 - ![]() , у колеса 2 -
, у колеса 2 - ![]() , у колеса 3 -
, у колеса 3 - ![]() На ободьях колес расположены точки А,В,С.
На ободьях колес расположены точки А,В,С.
В столбце «Дано» таблицы указан закон движения или закон изменения скорости ведущего звена механизма, где ![]() - закон вращения колеса 1,
- закон вращения колеса 1, ![]() - закон движения рейки 4,
- закон движения рейки 4, ![]() - закон изменения угловой скорости колеса 2,
- закон изменения угловой скорости колеса 2, ![]() - закон изменения скорости груза 5 и т.д. (везде
- закон изменения скорости груза 5 и т.д. (везде ![]() выражено в радианах,
выражено в радианах, ![]() - в сантиметрах,
- в сантиметрах, ![]() - в секундах). Положительное направление для
- в секундах). Положительное направление для ![]() и
и ![]() - против часовой стрелки, для
- против часовой стрелки, для ![]() - вниз.
- вниз.
Определить в момент времени ![]() = 1 с указанные в таблице в столбцах «Найти» скорости и ускорения соответствующих точек или тел. Вектора скоростей и ускорений указанных точек или тел изобразить на чертеже, также указать на чертеже круговые стрелки, соответствующие векторам угловых скоростей и угловых ускорений тел, которым принадлежат указанные точки.
= 1 с указанные в таблице в столбцах «Найти» скорости и ускорения соответствующих точек или тел. Вектора скоростей и ускорений указанных точек или тел изобразить на чертеже, также указать на чертеже круговые стрелки, соответствующие векторам угловых скоростей и угловых ускорений тел, которым принадлежат указанные точки.
Указания. Задача К1 – на исследование простейших движений твердого тела. При решении задачи учесть, что при зацеплении колес скорости точек зацепления одинаковы, а при ременной передаче скорости всех точек ремня и, следовательно, точек, лежащих на ободе этих колес одинаковы при отсутствии проскальзывания и растяжения ремня.
Таблица К1


Рис. К1.0 Рис. К1.1

Рис. К1.2 Рис. К1.3

Рис. К1.4 Рис. К1.5

Рис. К1.6 Рис. К1.7

Рис. К1.8 Рис. К1.9
Пример К1. Рейка 1, ступенчатое колесо 2 с радиусами ![]() и колесо 3 радиуса
и колесо 3 радиуса ![]() , скрепленное с валом радиуса
, скрепленное с валом радиуса![]() находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис. К.2). Рейка движется по закону
находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис. К.2). Рейка движется по закону ![]() .
.

Задача К2
Плоский механизм состоит из стержней 1,2,3,4, и ползуна В или Е. Точка D находится в середине стержня АВ. Длины стержней соответственно равны: ![]() . Положение механизма определяется углами
. Положение механизма определяется углами ![]() . Значения этих углов и других заданных величин указаны в таблице К2а или в таблице К2б, при этом в указанных таблицах
. Значения этих углов и других заданных величин указаны в таблице К2а или в таблице К2б, при этом в указанных таблицах ![]() - величины постоянные.
- величины постоянные.
Определить величины, указанные в таблицах в столбцах «Найти». Причем скорости указанных точек определить двумя способами: графоаналитическим, как показано в примере, и аналитическим.
Построение чертежа начинать со стержня, направление которого определяется углом ![]() ; ползун с направляющими для большей наглядности изобразить так, как в примере К2 (см. рис. К2б).
; ползун с направляющими для большей наглядности изобразить так, как в примере К2 (см. рис. К2б).
Заданные угловую скорость и угловое ускорение считать направленными против хода часовой стрелки, а заданные скорости ![]() и ускорение
и ускорение ![]() от точки В к b.
от точки В к b.
Указания. Задача К2 – на исследование плоскопараллельного движения твердого тела. При ее решении воспользоваться теоремами о скоростях и ускорениях точек плоской фигуры, а также понятием о мгновенном центре скоростей.
Таблица К2а (к рис. К2.0-К2.4)

Таблица К2б (к рис. К2.5-К2.9)


Рис. К2.0 Рис.К2.1

Рис.К2.2 Рис.К2.3

Рис.К2.4 Рис.К2.5

Рис.К2.6 Рис.К2.7

Рис.К2.8 Рис.К2.9
Пример К2. Механизм (рис.К2.а) состоит из стержней 1,2,3,4 и ползуна В, соединенных друг с другом и с неподвижными опорами ![]() шарнирами.
шарнирами.



Задача К3
Прямоугольная пластина (рис.К3.0-К3.4) или круглая пластина радиуса R=60 см (рис.К3.5-К3.9) вращается вокруг неподвижной оси по закону ![]() , заданному в таблице К3. Положительное направление отчета углов
, заданному в таблице К3. Положительное направление отчета углов ![]() показано на рисунках дуговой стрелкой. На рис. 0,1,2,5,6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 3,4,7,8,9 ось вращения
показано на рисунках дуговой стрелкой. На рис. 0,1,2,5,6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 3,4,7,8,9 ось вращения ![]() лежит в плоскости пластины (пластина вращается в пространстве).
лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой ВD (рис. 0-4) или по окружности радиуса R (рис. 5-9) движется точка М; закон ее относительного движения, т.е. зависимость ![]() (
( ![]() выражено в сантиметрах, t – в секундах), задан в таблице отдельно для рис.0-4 и для рис.5-9; там же даны размеры b и
выражено в сантиметрах, t – в секундах), задан в таблице отдельно для рис.0-4 и для рис.5-9; там же даны размеры b и ![]() . На рисунках точка М показана в положении, при котором
. На рисунках точка М показана в положении, при котором ![]() (при
(при ![]() точка М находится по другую сторону от точки А).
точка М находится по другую сторону от точки А).
Найти абсолютную скорость и абсолютное ускорение точки М в момент времени ![]() с.
с.
Указания. Задача К3 – на сложное движение точки. Для ее решения воспользоваться теоремами о сложении скоростей и сложении ускорений при сложном движении точки. Прежде чем проводить расчеты, следует по условию задачи определить, где находится точка М на пластине в момент времени ![]() , и изобразить точку именно в этом положении (а не в произвольном, как показано на рисунках к задаче)
, и изобразить точку именно в этом положении (а не в произвольном, как показано на рисунках к задаче)
В случаях, относящихся к рис. 5-9, при решении задачи не подставлять числового значения R, пока не будут определены положения точки М в момент времени ![]() и угол между радиусами СМ и СА в этот момент.
и угол между радиусами СМ и СА в этот момент.
Таблица К3


Рис. К3.0 Рис.К3.1 Рис. К3.2

Рис. К3.3 Рис.К3.4 Рис. К3.5

Рис.К3.6 Рис.К3.7

Рис.К3.8 Рис.К3.9
Пример К3 Шар радиуса R (рис К3.а) вращается вокруг своего диаметра АВ по закону![]() . По дуге большого круга («меридиану») АДВ движется точка М по закону
. По дуге большого круга («меридиану») АДВ движется точка М по закону![]() .
.


Рис. К3






