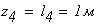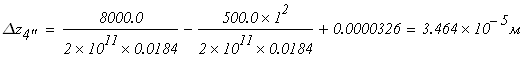Сопромат → растяжение - сжатие стержня расчет онлайн
Артикул: сопр2
Автор решения: admin
Расчет четырехступенчатого стержня. Задан ступенчатый стержень, нагруженный внешними сосредоточенными силами P и распределенными нагрузками q. Необходимо для…
Расчет четырехступенчатого стержня.
Задан ступенчатый стержень, нагруженный внешними сосредоточенными силами P и распределенными нагрузками q.
Необходимо для ступенчатого стержня выполнить следующее:
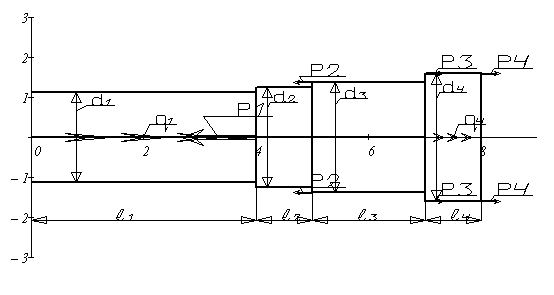
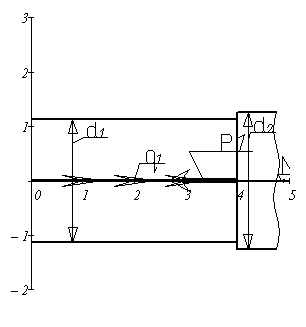
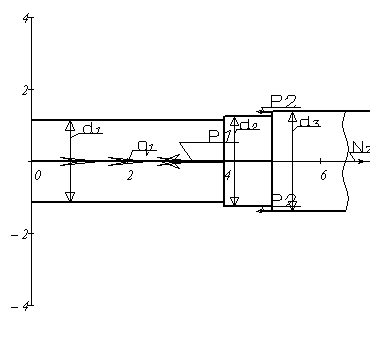
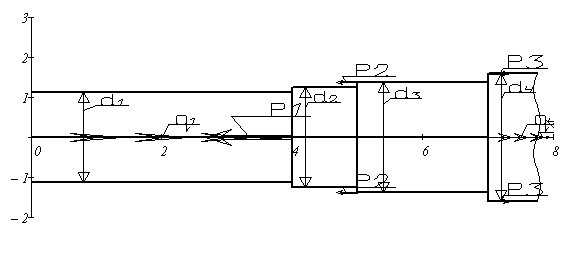
1. Начертить индивидуальную расчетную схему стержня.
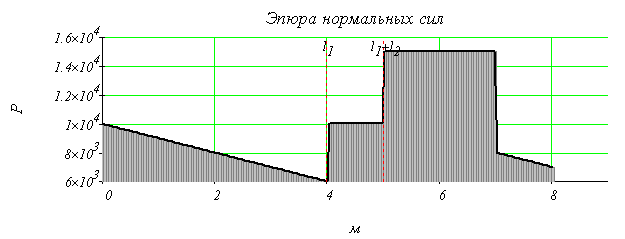
2. Построить эпюру нормальных сил.
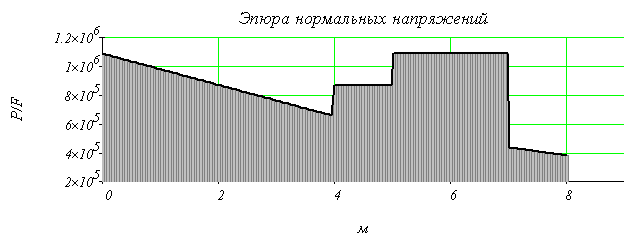
3. Построить эпюру нормальных напряжений
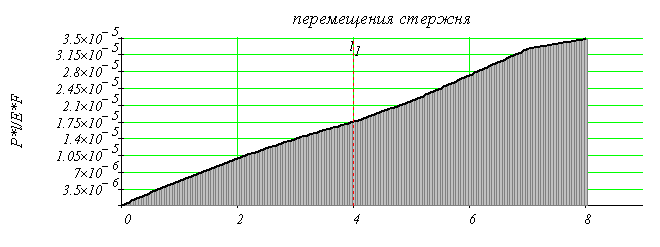
4. Построить эпюру перемещени
Решение задачи
Расчет на прочность и жесткость стержня при растяжении сжатии.
Задан ступенчатый стержень, нагруженный внешними сосредоточенными силами P и распределенными нагрузками q.
Необходимо для ступенчатого стержня выполнить следующее:
1. Начертить индивидуальную расчетную схему стержня.
2. Построить эпюру нормальных сил.
3. Построить эпюру нормальных напряжений
4. Построить эпюру перемещений.
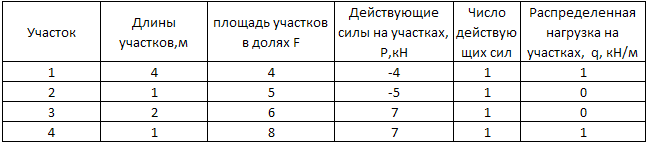
При расчетах принять:
Модуль упругости стержня при растяжении (сжатии) 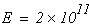
Предел текучести материала стержня 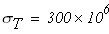
Допускаемое перемещение 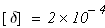
За площадь принять
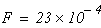
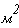
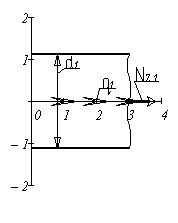
Решение: Вычерчиваем индивидуальную расчетную схему стержня, в соответствии с иходными данными.
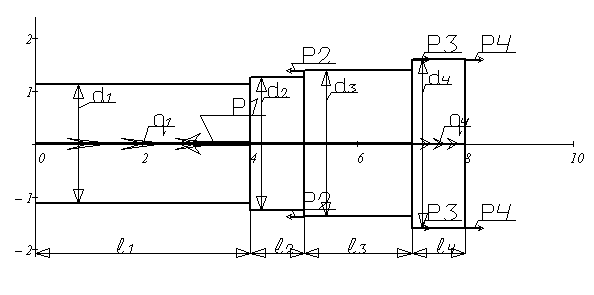
Определяем реакцию опоры из условия статичтического равновесия стержня
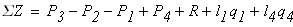
откуда получаем
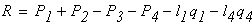
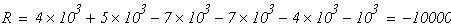
Используя метод сечений, определяем законы изменения нормальной силы на участках стержня.
Первый участок
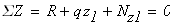
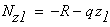
при
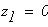
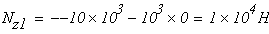
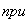
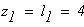
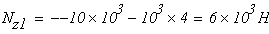
Второй учаток
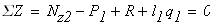
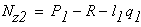
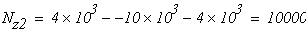
при
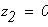
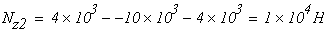
при
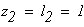
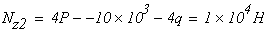
третий участок
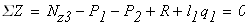
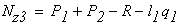
при
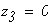
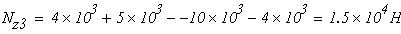
при
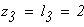
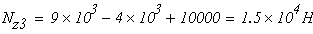
четвертый участок
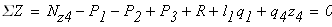
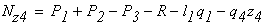
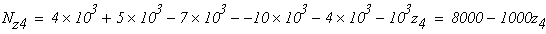
при
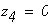
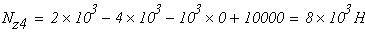
при
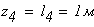
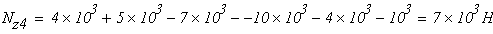
По полученным значениям 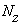
Вычисляем нормальные напряжения, действующие в поперечных сечениях, на участках стержня
Первый участок:
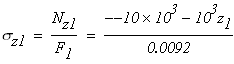
при
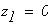
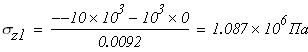
при
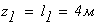
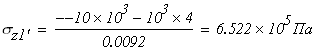
Второй участок:
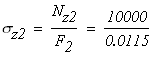
при
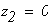
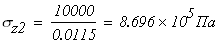
при
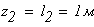
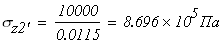
Третий участок:
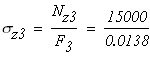
при
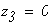
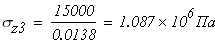
при
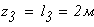
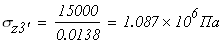
Четвертый участок
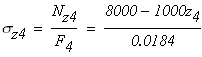
при
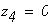
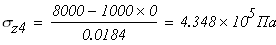
при
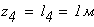
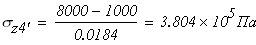
Используя закон Р. Гука в интегральной форме, находим перемещения на участках стержня.
Первый участок
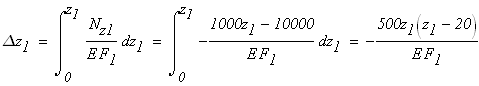
при
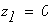
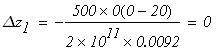
при
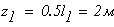
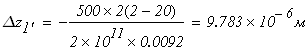
при
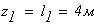
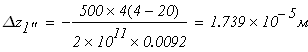
Второй участок
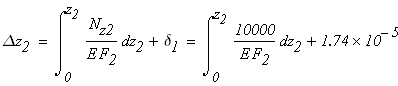
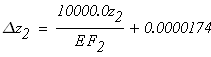
при
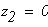
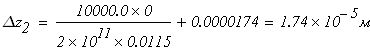
при
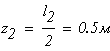
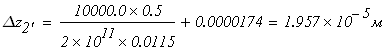
при
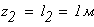
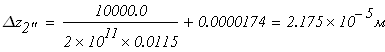
Третий участок
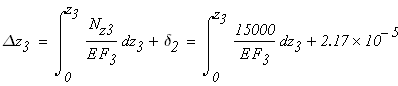
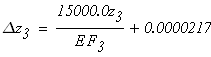
при
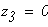
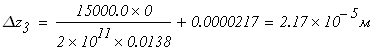
при
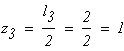
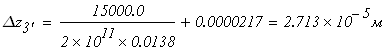
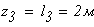
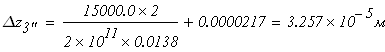
Четвертый участок
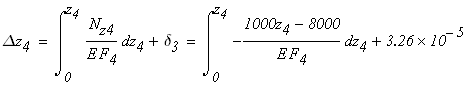
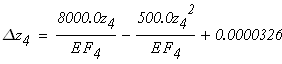
при
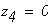
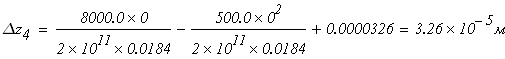
при
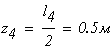
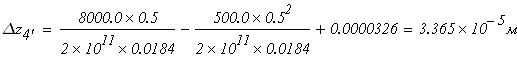
при