Механика и молекулярная физика. формулы и пояснения.

МЕХАНИКА И МОЛЕКУЛЯРНАЯ ФИЗИКА

 

Основные законы и формулы.

 

Скорость мгновенная  v =  или v = ,   где dх или dS – путь, проходимый точкой за время dt.

 Ускорение мгновенное, тангенциальное а_τ =  = ,

Нормальное ускорение  a_n = v² /r,  полное ускорение  a = , где r – радиус кривизны траектории.

Путь при равноускоренном движении тела .

Угловая скорость  ω = ,   где dφ – угол поворота тела за время dt.

Угловое ускорение ε =  . Уравнения равнопеременного вращательного движения  ω = ω₀ + εt; φ = ω ₀t+ εt²/2,  где ω₀ – начальная угловая скорость.

Связь между линейными угловыми величинами при движении точки

по окружности s = φr;  v = ωr;  a_τ = εr;  a;  Т = 1/ν;  ω = 2πν, где T – период, ν – частота вращения.

Импульс точки массы m, движущейся со скоростью v определяется р = mv,

Второй закон Ньютона для поступательного движения   = m,

где  – векторная сумма действующих на тело сил.

Закон сохранения импульса для изолированной системы .

Сила трения скольжения f_тр = μF_n, где F_n — сила нормального давления, μ - коэффициент трения.

Скорости шаров массами m₁ и m₂ после центрального удара:

- абсолютно упругого: ; ;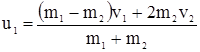

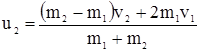 - абсолютного неупругого : 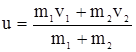 , где v₁ и v₂ – скорости шаров массой m₁и m₂ до удара.

Работа переменной силы на пути , где α – угол между векторами  и d.   Мощность

Сила упругости: F = - kx, где k – коэффициент жесткости упругого элемента.

Потенциальная энергия упругодеформированного тела: W_П = kx²/2,

Сила гравитационного притяжения: F = Gm₁m₂/r², где G – гравитационная постоянная, r – расстояние между телами m₁ и m₂.

Потенциал гравитационного поля Земли: j  = GM_З/(R₃ + h),

Напряженность гравитационного поля Земли: Е = GM_З/(R₃ + h)², где М_З – масса и R_з – радиус Земли, h – высота точки над поверхностью Земли.

Потенциальная энергия тела в поле земного тяготения вблизи поверхности:            W_П = mgh,  где g — ускорение свободного падения, h – высота тела

над поверхностью Земли.

Кинетическая энергия движущегося тела:Т = mv²/2 = р²/2m,

Закон сохранения механической энергии: W = Т +W_П = const.

Момент инерции материальной точки относительно оси: J = mR², где R - расстояние от точки массой m до оси вращения.

Моменты инерции некоторых тел массой m:

 - сплошного однородного цилиндра (диска) относительно оси вращения

   J = mR²/2,  полого цилиндра относительно оси вращения - J = mR²,  шара относительно центра  - J = 0,4mR², где R - радиус цилиндра или шара,

 - стержня длиной l, ось вращения которого перпендикулярна стержню

   и проходит через его центр масс J₀ = ml²/12, стержня длиной l, ось вращения которого проходит через один из концов стержня J = ml²/3,

 -тела c моментом инерции J₀ относительно произвольной оси вращения

  (теорема Штейнера): J = J_o + md², где d – расстояние от оси вращения до центра масс тела.

Момент силы относительно оси вращения M = Fd, где d - плечо силы, т.е. кратчайшее расстояние от оси вращения до линии действия силы.

Основное уравнение динамики вращательного движения: M = ,

где  L = Jω – момент импульса тела. То же, но при J = const   M = J = Jε,

Закон сохранения момента импульса:                                    = const.

Кинетическая энергия вращающегося тела:                                 T = Jω²/2,

Работа при вращательном движении:                                               dA = Mdφ,

Энергия покоя частицы массой m₀:      E₀ = m₀c²,  где с – скорость света.

Зависимость от скорости v в релятивистской механике:  

 -импульса частицы:  р = 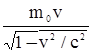,   длины тела:   l = ,

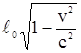  времени:  t = 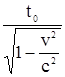, кинетической энергии: T = E – E₀ =m₀c²,

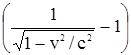 - полной энергии частицы:                                         E = mc² = ,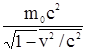

Теорема сложения скоростей в теории относительности:   u^/ = ,

где u^/ - скорость тела в инерциальной системе К^/, которая движется со скоростью v относительно инерционной системы К, в которой тело движется со скоростью u.

Количество вещества:   ν =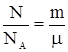, где N – число молекул, N_А – число Авогадро, m – масса вещества, μ – молярная масса. Уравнение Клапейрона – Менделеева:  pV = RT, где р – давление газа, V – его объем, R –универсальная газовая постоянная, T – термодинамическая температура.   Уравнение молекулярно – кинетической теории газов:

p = , где n = N/V – концентрация молекул,

<E_к> - средняя кинетическая энергия поступательного движения молекул,

 m₀ – масса, <υ_кв> - среднеквадратичная скорость молекулы.

Закон Дальтона для смеси газов: р = , где p_i – парциальные давления компонентов смеси. Средняя кинетическая энергия молекул:  <E_к> = ,

где i – число степеней свободы молекулы, k – постоянная Больцмана.

Внутренняя энергия идеального газа:                                   U = .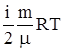

Скорости молекул:  среднеквадратичная:               <v_кв> =,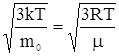

 - среднеарифметическая:                                             <v> =,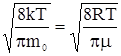

 - наиболее вероятная:                                                       v_в =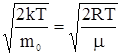

Средняя длина свободного пробега молекулы:                <λ> =,

где d – эффективный диаметр молекулы.

Среднее число столкновений молекул в един. времени: <z> =.

Уравнение диффузии: dm = -DdSdt, где – коэффициент диффузии, ρ – плотность, dS- элементарная площадка, перпендикулярная оси Х,  - градиент  плотности. Уравнение теплопроводности:  dQ = - χ,

где χ = c_v ρ– коэффициент теплопроводности, с_v – удельная  теплоемкость при постоянном объёме,  - градиент температуры.

Сила внутреннего вязкого трения: ,  где  – динамическая вязкость,  - градиент скорости.

Удельная теплота плавления:  r = . Удельная теплота парообразования:                                                    λ = . Удельная теплоемкость газа:      С_уд = .

Молярная теплоемкость идеального газа:  С=.

 

     - изохорная:   ,  изобарная:                 .

Уравнение первого начала термодинамики:                     dQ = dU + dA,

где dU = C_vdT,  dA = pdV.

Работа расширения газа при процессах:

  - изобарный:                                                    ;

  - изотермический:                                              ;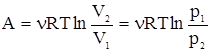

 

 

 

 - адиабатический:

     ,

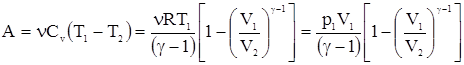где  = (i + 2)/i – показатель адиабаты или коэффициент Пуассона.

Уравнения адиабатического процесса:

  ; ; .

Коэффициент полезного действия тепловой машины:   η = .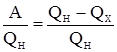

Коэффициент полезного действия цикла Карно:     ,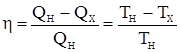

где Q_Н и T_Н – количество теплоты, полученное от нагревателя, и его температура, Q_Х и T_Х – количество теплоты, переданное охладителю, и его температура.

Изменение энтропии при обратимом переходе системы из состояния 1 в состояние 2: .