Артикул: avt001
Автор решения: admin
Задача содержит вопросы по исследованию систем автоматического регулирования (САР) на определение их устойчивости по различным критериям. Замкнутая система…
Задача содержит вопросы по исследованию систем автоматического регулирования (САР) на определение их устойчивости по различным критериям.
Замкнутая система автоматического регулирования состоит из 3-х последовательно соединенных звеньев
Второе звено охвачено местной обратной связью. Определить устойчивость системы по критерию Гурвица и по критерию Михайлова. Автоматическая система регулирования - замкнутая САР (система автоматического регулирования) состоит из 3-х последовательно соединенных звеньев. Второе звено охвачено местной обратной связью. Определить устойчивость системы по заданному критерию Гурвица.
Ссылка на устойчивость по критерию Михайлова
Решение задачи
Задача 2
Передаточные функции звеньев рис. 1 имеют вид:
1.
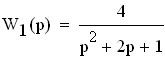
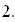
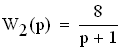
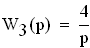
Передаточная функция местной обратной связи
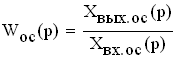
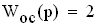
Изображаем схему алгоритмической структуры автоматической системы регулирования.
Зная передаточные функции звеньев, несложно получить общую передаточную функцию разомкнутой АСУ -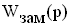 
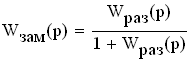
, а затем получить и передаточную функцию замкнутой АСУ - Wзам(р)
Здесь в знаменателе знак (+) при отрицательной обратной связи. В случае положительной обратной связи в знаменателе между слагаемыми останется знак «минус».
Находим общую передаточную функцию для разомкнутой АС (автоматической системы), для чего имеющуюся замкнутую АС разомкнем (этот разрыв можно сделать между любыми другими звеньями) в точке Q.
В этой задаче местная обратная связь положительная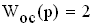 
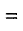
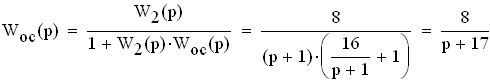
и передаточная функция второго звена определяется уравнением:
Общая передаточная функция для последовательной разомкнутой системы будет равна:
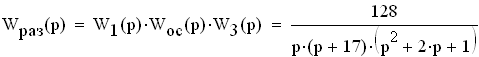
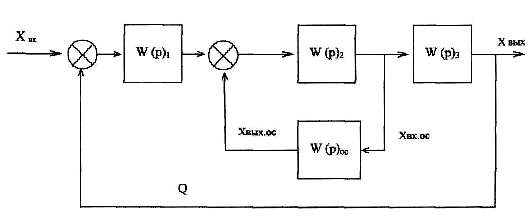
Рис.1. Схема алгоритмической структуры автоматической сисьемы регулирования
Определение устойчивости САР по критерию Гурвицу
Чтобы определить устойчивость САР по критерию Гурвица, необходимо вначале найти характеристическое уравнение для разомкнутой САР.
Передаточная функция для разомкнутой системы получена выше:
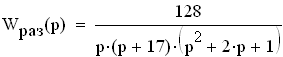
Для замкнутой сисьемы в случае отрицательной обратной связи передаточная функция будет равна:
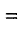
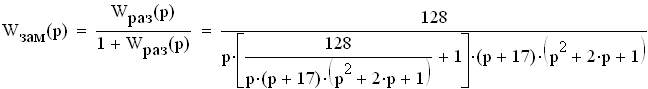
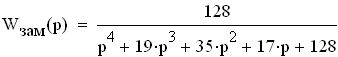
где знаменатель есть характеристическое уранение для замкнутой САР, Т.е.
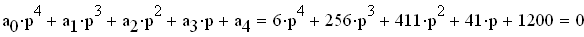
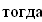
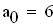
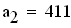
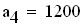
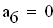
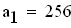
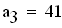
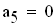
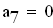
Определитель Гурвица определяется следующим образом. Все коэффициенты от a1 до а4 располагаются в главной диагонали в порядке возрастания индексов. Вверх от главной диагоналя в столбцах записываются коэффициенты характеристического уравнения с последовательно возрастающими, а вниз - убывающими индексами. На месте коэффициентов, индексы которых больше 4 , и меньше чем нуль, проставляются нули: составляем определитель из коэффициентов характеристического уравнения:
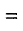
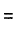
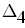
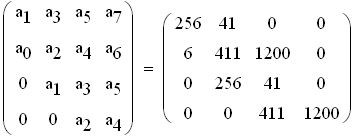
Находим величины 2-го ранга и последнего(в нашем случае 3-го) диагональных миноров:
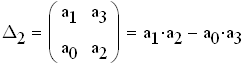
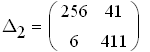
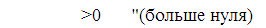
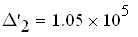
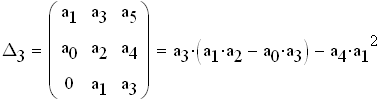
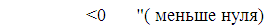
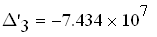
по критерию Гурвица система устойчива только тогда, когда все коэффициенты опрелителя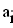 
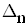
и все диагональные миноры определителя 
больше нуля.
Вывод: