Артикул: нтр26
Автор решения: testadmin
Задание 1. Содержание задания: испытания проводились для N0 изделий, из них за время t часов отказало n(t) штук, ещё через Δt часов отказало n(Δt)…
Задание 1.
Содержание задания: испытания проводились для N0 изделий, из них за время t часов отказало n(t) штук, ещё через Δt часов отказало n(Δt) изделий. Определите Q(t), Р(t), Р(t+Δt), f(t), λ(t).
Задание 2.
Испытания проводились для N0 неремонтируемых изделий. Через каждые Δt часов фиксировалось число отказов n(Δti), данные указаны в таблице 3. Постройте зависимость интенсивности отказов изделий от времени испытания.
Задание 3.
За период эксплуатации устройство отказало 10 раз. Время его восстановления после каждого отказа указано в таблице. Определите среднее время восстановления.
Задание 4.
Параметр потока отказов и интенсивность восстановления системы управления величины постоянные и равны ω и μ соответственно. Определите для системы среднюю наработку на отказ, среднее время восстановление и коэффициент готовности.
Задание 5.
Вероятность того, что за 10 лет эксплуатации диод не откажет равна p. Определите вероятность того, что за этот же период времени из 10 диодов откажет:
1. ровно k диодов;
2. не более, чем k диодов.
Задание 6.
Вероятность того, что изделие имеет дефект равна p. Определите вероятность того, что из n изделий k будут иметь дефект.
Задание 7.
Время безотказной работы электроустановки подчинено экспоненциальному закону распределения. Определите вероятность безотказной работы, вероятность отказа для времени t и среднюю наработку до отказа, если интенсивность отказов равна λ.
Задание 8.
Система состоит из 4 элементов, время безотказной работы которых подчинено экспоненциальному закону распределения с интенсивностью отказов λ1, λ2, λ3, λ4. Отказ любого из элемента системы приведёт к отказу всей системы. Определите среднюю наработку до отказа системы и её вероятность того, что система проработает безотказно 2 года (17520 ч). Сравните вероятность безотказной работы системы с вероятностями безотказной работы элементов. Сделайте вывод.
Задание 9.
Кабельная линия обладает простейшим потоком отказов с интенсивностью отказа λ. Определите вероятность безотказной работы для момента времени t в случае, если:
1. среднее время восстановления Tв (μ=const);
2. линия не подлежит восстановлению.
Задание 10
Система состоит из 3 равнонадёжных невосстанавливаемых элементов, время до отказа которых подчиняется экспоненциальному закону распределения с интенсивностью отказа λ. Определите вероятность безотказной работы для момента времени t и среднюю наработку до отказа, если:
1. система не имеет резерва;
2. система имеет общее постоянной резервирование, с кратностью резервирования m=1;
3. система имеет общее резервирование с замещением, той же кратности;
4. каждый элемент системы имеет собственный резервирующий элемент.
Надёжность резервирующих элементов считать равным надёжности основных. Определите выигрыш надёжности по вероятности безотказной работы. Сделайте вывод.
Задание 11.
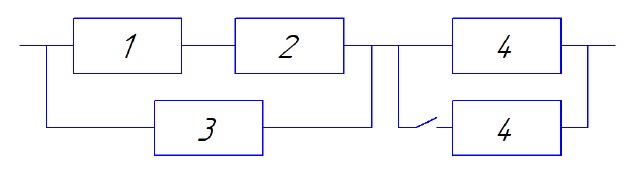
На рисунке изображена блок-схема надёжности электрической цепи. Вероятность выхода элементов цепи из строя Q1, Q2, Q3, Q4 за время t, приведена в таблице. Определите вероятность разрыва цепи, если вероятность выходя из строя любого из элементов не оказывает влияние на вероятность отказа других элементов.
Задание 12.
Система управления включает в себя три одинаковых равнонадёжных датчика. За верное значение измеряемой величины система принимает значение, поступившее с большинства датчиков. Определите вероятность безотказной работы системы для момента времени t и среднюю наработку до отказа, если известна интенсивность отказа датчика λ (считая, что время до отказа подчиняется экспоненциальному закону распределения).
Выполнен вариант - 26
Количество страниц - 18
Формат документа - pdf
<в каталог
Цена: 850.00р.