Внимание! Размещенный на сайте материал имеет информационно - познавательный характер, может быть полезен студентам и учащимся при самостоятельном выполнении работ и не является конечным информационным продуктом, предоставляемым на проверку.

Сопромат. Заочники.

 <в каталог

Задача 1. 

Для стержня (рис. 1) постоянного сечения следует:

№ строки

№ схемы

Р, кН

а, м

Е, МПа

1

I

30

1,1

1,2∙105

2

II

20

1,2

1,4∙105

3

III

25

1,3

1,5∙105

4

IV

30

1,4

1,6∙105

5

V

40

1,5

1,7∙105

6

VI

48

1,6

1,8∙105

7

VII

64

1,7

1,9∙105

8

VIII

80

1,8

2,0∙105

9

IX

90

1,9

2,1∙105

0

X

60

2,0

2,2∙105

 

в

а

б

а

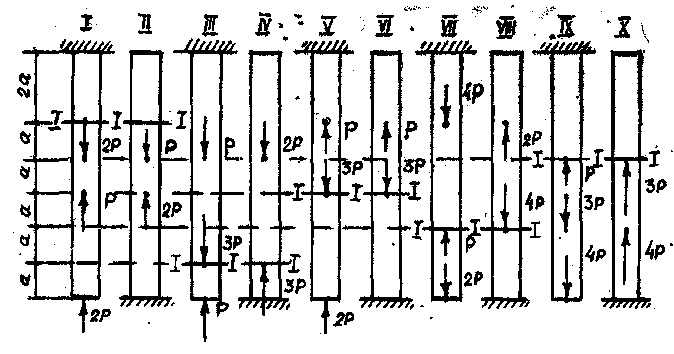
1. Построить эпюру продольных сил N, напряжений σ, относительных деформаций ε и перемещений сечений ∆ℓ.

2. Выписать выражение наибольшего по модулю нормального напряжения σmax и из условия прочности определить необходимую площадь сечения F, приняв [σ]=160 МПа.

3. Определить перемещение сечения I-I.

4. Составить раскрытые выражения потенциальной энергии  U в брусе.

Данные взять из таблицы 1.

 

Задача 2

Статически неопределимая стержневая конструкция.

Для системы, состоящей из абсолютно жесткого бруса и упругих стержней, требуется:

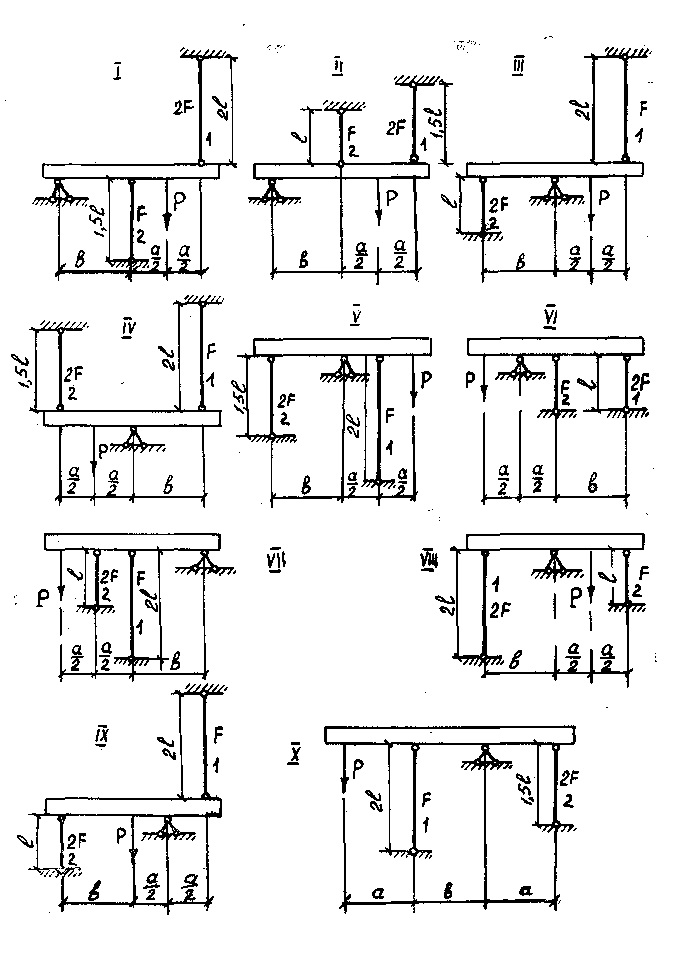
1. Определить усилия в стержнях, поддерживающих абсолютно жесткую балку (см. рисунок 2), от нагрузки Р.

2. Вычислить напряжения в стержнях от нагрузки Р.

3.  Из условия прочности, определить необходимую площадь F поперечного сечения стержней, приняв [σ]=200 МПа.

Материал стержней – сталь. Данные взять из таблицы 

№ строки

№ схемы

а, м

в, м

ℓ, м

Р, кН

1

I

2,1

1,1

1,8

21

2

II

2,2

1,2

1,7

22

3

III

2,3

1,3

1,6

23

4

IV

2,4

1,4

1,5

24

5

V

2,5

1,5

1,4

25

6

VI

2,6

1,6

1,3

26

7

VII

2,7

1,7

1,2

27

8

VIII

2,8

1,8

1,1

28

9

IX

2,9

1,9

1,0

29

0

X

2,0

1,0

1,9

20

 

в

а

б

в

в

 

 

Задача 3 

На рисунке 3 приведены схемы балок.

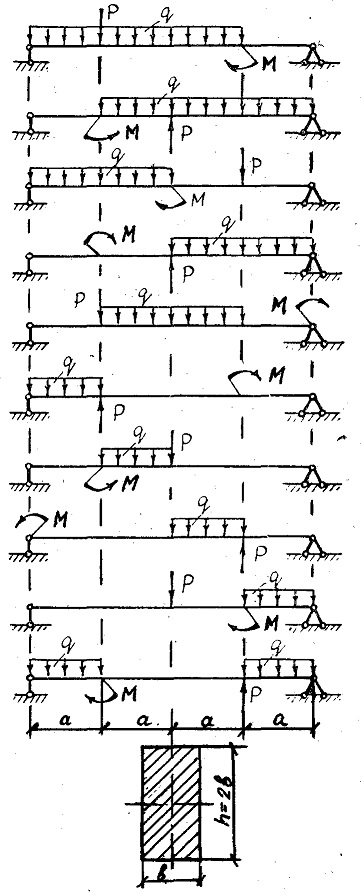Требуется:

1. Построить эпюры изгибающих моментов и поперечных сил.

2. Подобрать сечение в виде прямоугольника (h=2b), приняв [σ]=160 МПа.

3. Построить эпюру нормальных напряжений в опасном сечении.

Данные взять из таблицы 3.

Принять интенсивность равномерно распределенной нагрузки q=6 кН/м.

 

№ строки

№ схемы

а, м

Р, кН

М, кН∙м

1

I

1,5

10

150

2

II

2,0

15

200

3

III

2,5

20

120

4

IV

3,0

25

100

5

V

3,5

30

300

6

VI

4,0

35

180

7

VII

4,5

40

60

8

VIII

5,0

45

240

9

IX

5,5

50

220

0

X

6,0

60

160

 

в

а

б

в

 

 

 

 

 

Задача 4

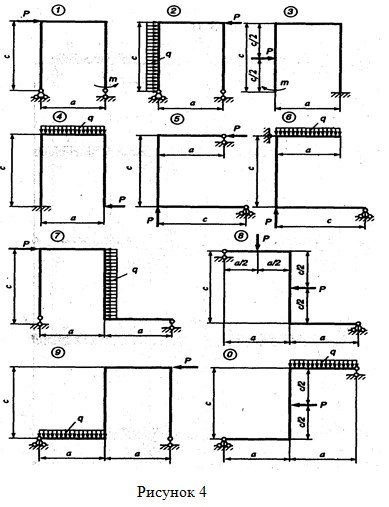
Изгиб рам.
Для схемы рамы требуется:
1. Составить аналитические выражения изменения продольной силы Nx, поперечной силы Qy, изгибающего момента Mz.
2. Построить эпюры внутренних силовых факторов (э Nx, э Qy, э Mz).
3. По опасному сечению подобрать диаметр d поперечного сечения.
Исходные данные взять из таблицы.

№ строки

№ схемы

с/a

P/qa

m/qa2

a,м

q, кН/м

1

1

1,2

0,6

0,2

0,5

6

2

2

1,4

0,5

0,4

1,0

8

3

3

1,6

0,8

0,6

1,5

10

4

4

1,8

1,2

0,8

2,0

12

5

5

2,0

1,5

1,0

2,5

14

6

6

1,2

1,6

0,2

1,5

16

7

7

1,4

1,0

0,4

2,0

12

8

8

1,6

1,8

0,6

1,0

10

9

9

1,8

2,4

0,8

2,5

8

0

0

2,0

2,0

1,0

0,5

6

 

в

а

б

в

б

а

 

 

 

 

Задача 5

Кручение валов.

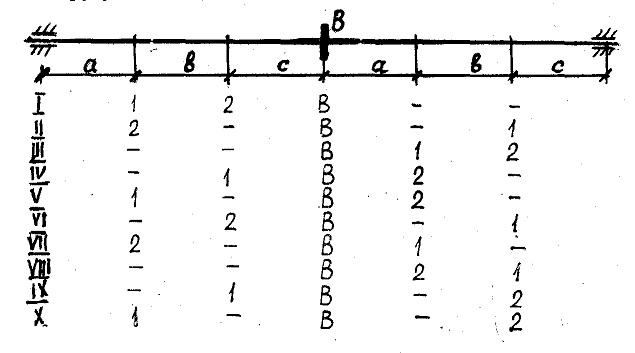
На приводном валу (см. рис. 4) установлен ведущий шкив В и два рабочих 1 и 2, от которых последовательно берутся мощности: N1, N2 кВт. Требуется:

1. Построить эпюру крутящих моментов.

2. По заданным [τ] и [φ] определить необходимый диаметр сплошного вала и округлить его до ближайшей величины, соответственно равной 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 125, 140, 160, 180, 200 (мм).

3. Построить эпюру углов закручивания вала.

Данные взять из таблицы 4.

№ строки

№ схемы

а, м

в, м

с, м

N1, кВт

N2, кВт

n0, об/мин

[φ], град

[τ], МПа

1

I

1,0

1,5

2,0

40

130

600

2

100

2

II

1,2

1,6

1,8

50

120

900

3

120

3

III

1,4

1,7

1,6

60

110

1200

4

140

4

IV

1,6

1,8

1,4

70

100

1500

3

160

5

V

1,8

2,0

1,2

80

90

1200

2

180

6

VI

2,0

1,8

1,4

90

80

900

3

200

7

VII

1,8

1,7

1,6

100

70

600

4

180

8

VIII

1,6

1,6

1,8

110

60

900

3

160

9

IX

1,4

1,5

2,0

120

50

1200

2

140

0

X

1,2

1,4

2,2

130

40

1500

4

120

 

в

б

а

в

а

в

б

а

в

Задача 6.

Косой изгиб.

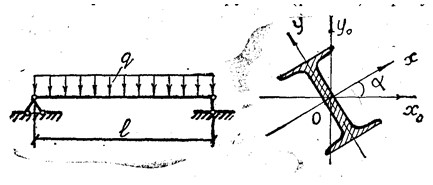
Балка двутаврового профиля, повернутая на угол α относительно вертикали, загружена равномерно распределенной вертикальной нагрузкой q (рис. 6). Требуется:
1. Определить положение нулевой линии в опасном сечении.
2. Определить величину наибольшего нормального напряжения.
3. Вычертить опасное сечение балки и показать на нем нулевую линию, эпюру нормальных напряжений.
Данные взять из таблицы.

№ строки

q, кН/м

ℓ, м

α, град

№ двутавра

1

5,0

1,6

4

32

2

4,5

2,0

5

30

3

4,0

2,4

6

28

4

3,5

3,2

8

26

5

3,0

4,0

10

24

6

2,5

4,8

12

22

7

2,0

5,6

15

20

8

1,5

6,4

16

18

9

1,0

7,2

18

16

0

0,5

8,0

20

14

 

в

б

в

а

Задача 7.

Совместное действие изгиба и кручения.
На валу насажены зубчатые колеса. К колесам приложены окружные усилия Р1, Р2, Р3. Требуется:

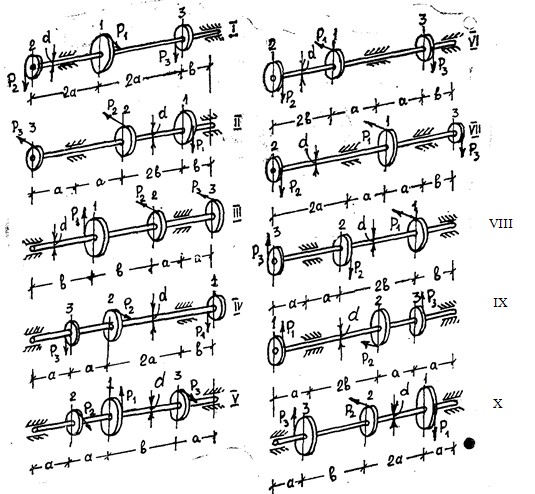1. Из условия равновесия ∑Мх=0 определить величину Р1 или Р3.
2. Определить крутящие моменты и построить эпюру крутящих моментов.
3. Определить силы, изгибающие вал в вертикальной и горизонтальной плоскости.
4. Построить эпюры изгибающих моментов от горизонтальных сил Му, и от вертикальных сил Мz.
5. При помощи эпюр найти опасное сечение и определить величину максимального расчетного момента.
6. Подобрать диаметр вала по III теории прочности – теории наибольших касательных напряжений.
Данные взять из таблицы.

№ строки

№ схемы

Р1, кН

Р2, кН

Р3, кН

[σ], кН/см2

а, см

b, см

Диаметры зубчатых колес, см

D1

D2

D3

1

I

-

6

10

10

40

50

40

40

20

2

II

8

5

-

9

50

40

50

40

20

3

III

-

7

9

10

40

30

40

30

30

4

IV

6

8

-

10

50

40

60

30

20

5

V

-

6

11

10

30

50

50

50

30

6

VI

5

8

-

9

20

30

30

30

20

7

VII

-

5

10

9

30

40

40

20

10

8

VIII

4

7

-

11

50

20

20

20

10

9

IX

-

6

11

10

30

50

30

30

20

0

X

8

6

-

9

40

30

50

20

10

 

в

б

б

б

а

в

б

б

а

а

 

Задача 8.

Расчет сжатых стержней на устойчивость.
Стальной стержень длиной ℓ сжимается силой Р.
Требуется:
1. Найти размеры поперечного сечения при допускаемом напряжении на простое сжатие [σ]=160 МПа (расчет производить последовательным приближением, предварительно задавшись величиной коэффициента φ=0,5).
2. Найти величину критической силы и коэффициент запаса устойчивости.
Данные взять из таблицы.

Значение коэффициента продольного изгиба j в зависимости от гибкости λ

l

0

20

40

60

80

100

120

140

160

180

200

j

1,00

0,96

0,92

0,86

0,75

0,60

0,45

0,36

0,29

0,23

0,19

 

Таблица с готовыми вариантами

вариант №001 вариант №021 вариант №041 вариант №061 вариант №081
вариант №002 вариант №022 вариант №042 вариант №062 вариант №082
вариант №003 вариант №023 вариант №043 вариант №063 вариант №083
вариант №004 вариант №024 вариант №044 вариант №064 вариант №084
вариант №005 вариант №025 вариант №045 вариант №065 вариант №085
вариант №006 вариант №026 вариант №046 вариант №066 вариант №086
вариант №007 вариант №027 вариант №047 вариант №067 вариант №087
вариант №008 вариант №028 вариант №048 вариант №068 вариант №088
вариант №009 вариант №029 вариант №049 вариант №069 вариант №089
вариант №010 вариант №030 вариант №050 вариант №070 вариант №090
вариант №011 вариант №031 вариант №051 вариант №071 вариант №091
вариант №012 вариант №032 вариант №052 вариант №072 вариант №092
вариант №013 вариант №033 вариант №053 вариант №073 вариант №093
вариант №014 вариант №034 вариант №054 вариант №074 вариант №094
вариант №015 вариант №035 вариант №055 вариант №075 вариант №095
вариант №016 вариант №036 вариант №056 вариант №076 вариант №096
вариант №017 вариант №037 вариант №057 вариант №077 вариант №097
вариант №018 вариант №038 вариант №058 вариант №078 вариант №098
вариант №019 вариант №039 вариант №059 вариант №079 вариант №099
вариант №020 вариант №040 вариант №060 вариант №080 вариант №100