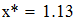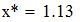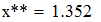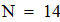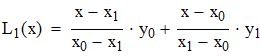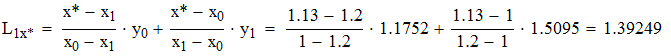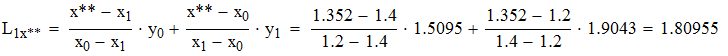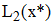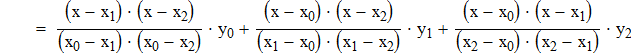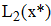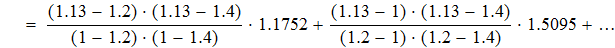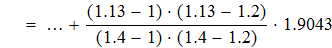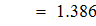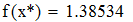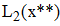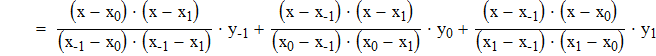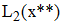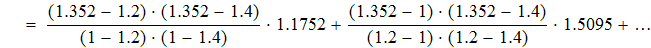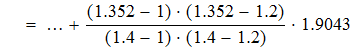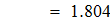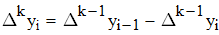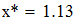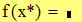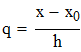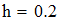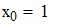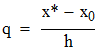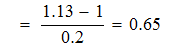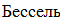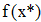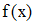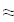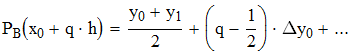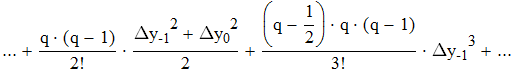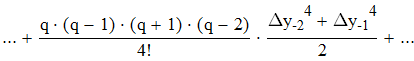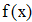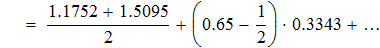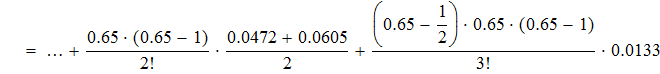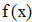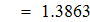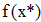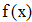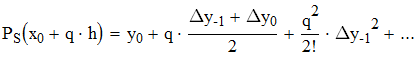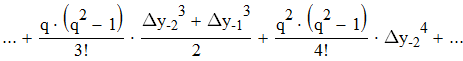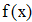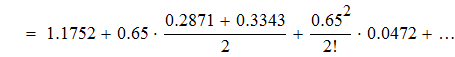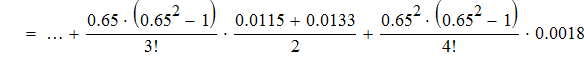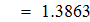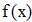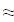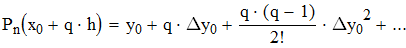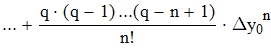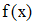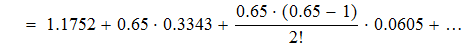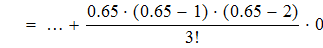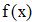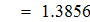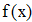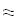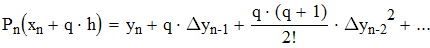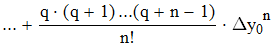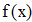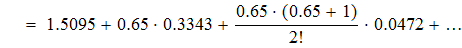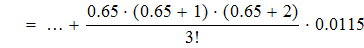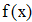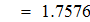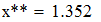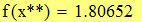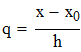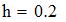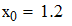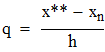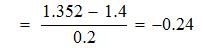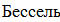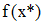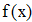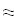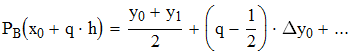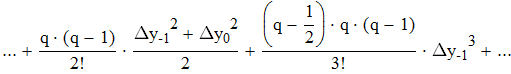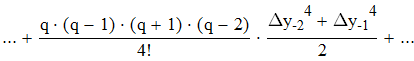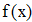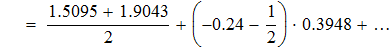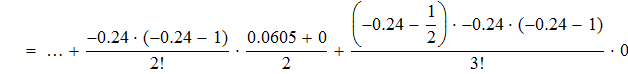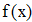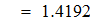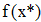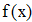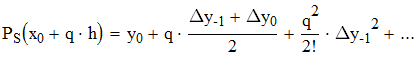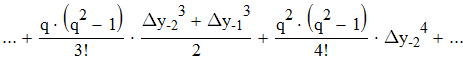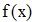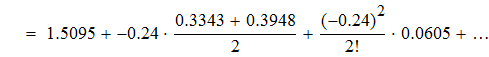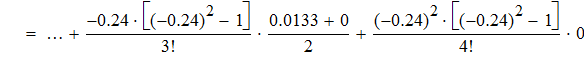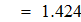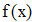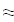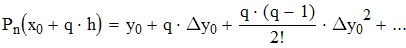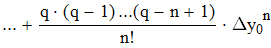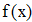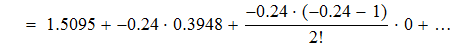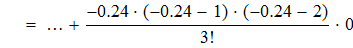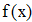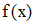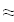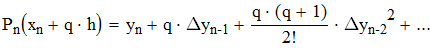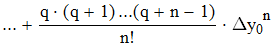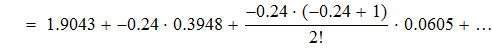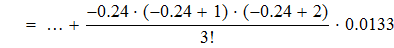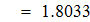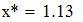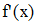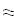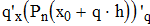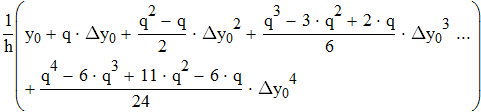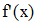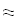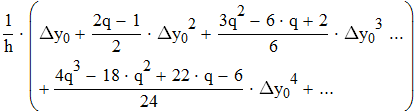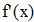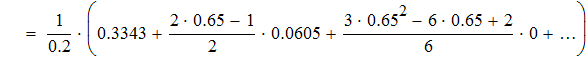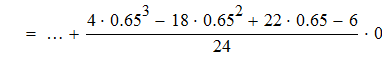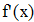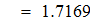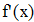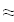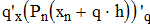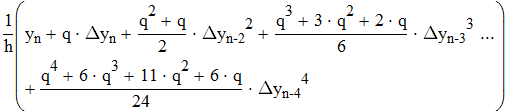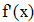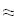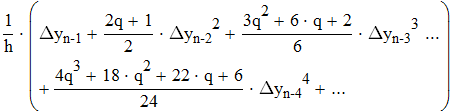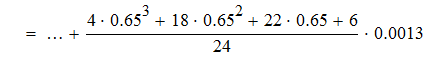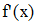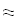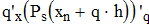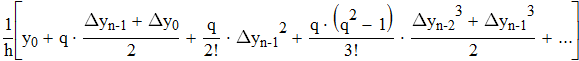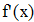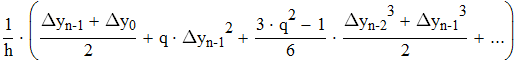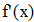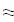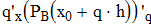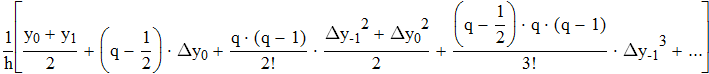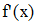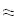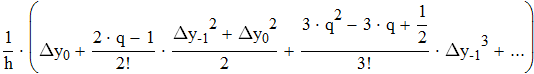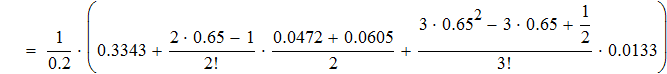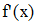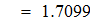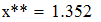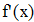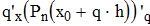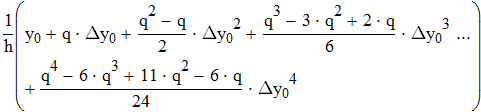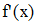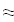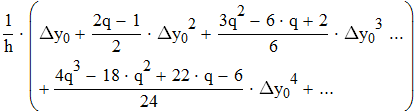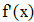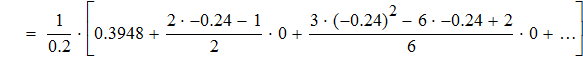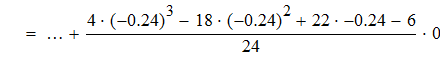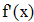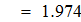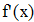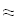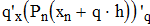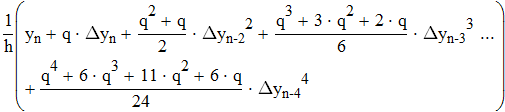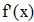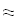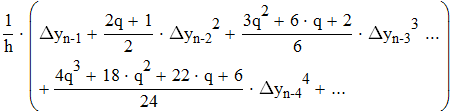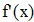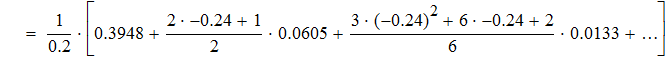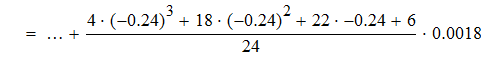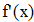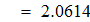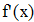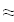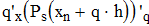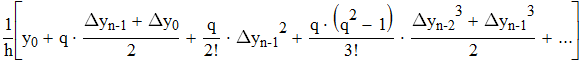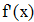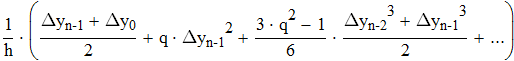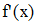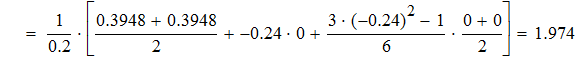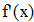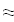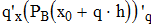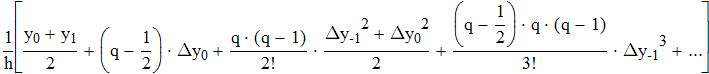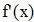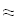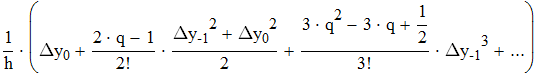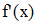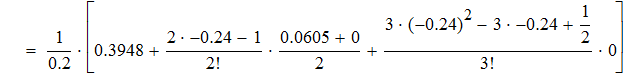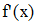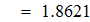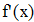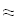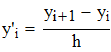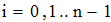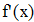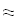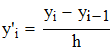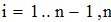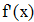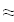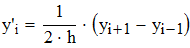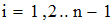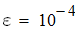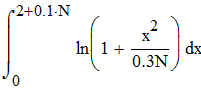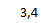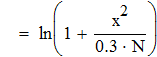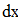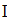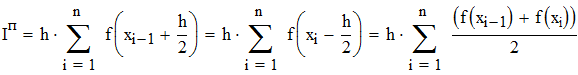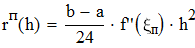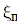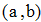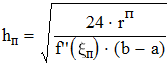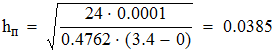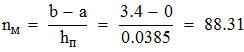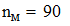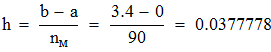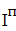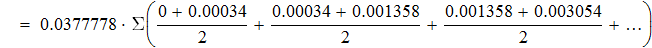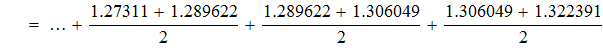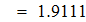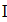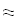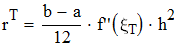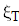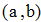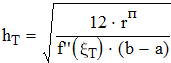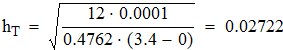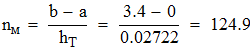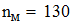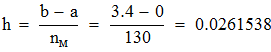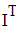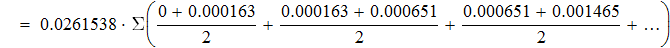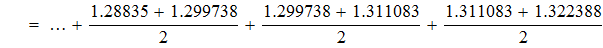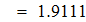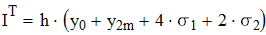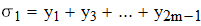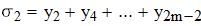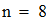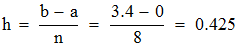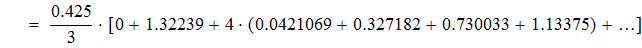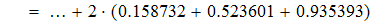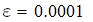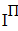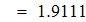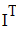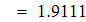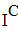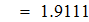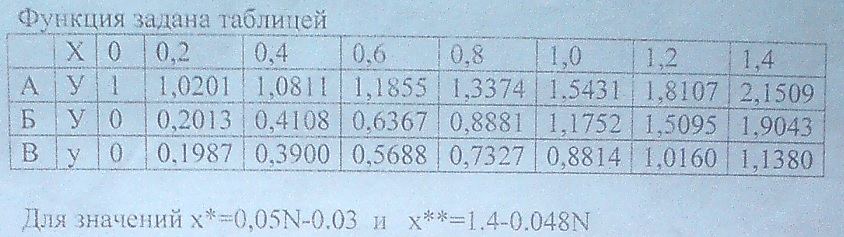
Найти значения y(x*) и y(x**) пользуясь:
Лабораторная работа №1.
-
Линейной и квадратичной интерполяцией Лагранжа, оценить погрешность.
-
Выбрть подходящую интерполяционную формулу Ньютона, Бесселя, или Стирлинга для вычисления функции.
Лабораторная работа №2.
1. В точках x* и x** из ЛР№1 вычислить производную функции, дифференциируя интерполяионные формулы.
2. Создать таблицу с приближенными значениями f(x) которые находим по формулам:
а) первого поряка точности;
б) второго порядка точности.
Лабораторная работа №3.
Вычислить интеграл с точностью 0,0001 методами прямоугольников, трапеций и Симпсона.
Лабораторная работа №1
Лабораторная работа №2
Лабораторная работа №3
Найдем значения y(x*) и y(x**) пользуясь:
1) Линейной и квадратичной интерполяцией Лагранжа
2) Выбрать подходящую интерполяционную формулу Ньютона, Бесселя, или Стирлинга для вычисления функции
1. Нахождение линейной и квадратичной интерполяции Лагранжа
Используя формулу линейной интерполяции Лагранжа, находим значение y(x*) и y(x**)
Используя формулу квадратичной интерполяции Лагранжа, находим значение y(x*) и y(x**)
2. Выбор подходящей интерполяционной формулы Ньютона, Бесселя или Стирлинга для вычисления значения функции. Нахождение значений функции.
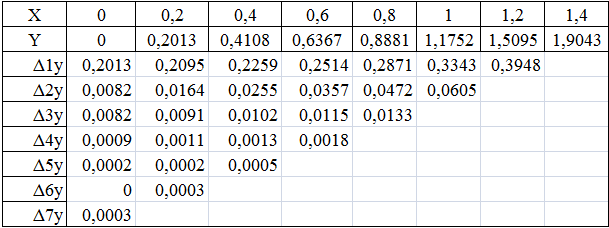
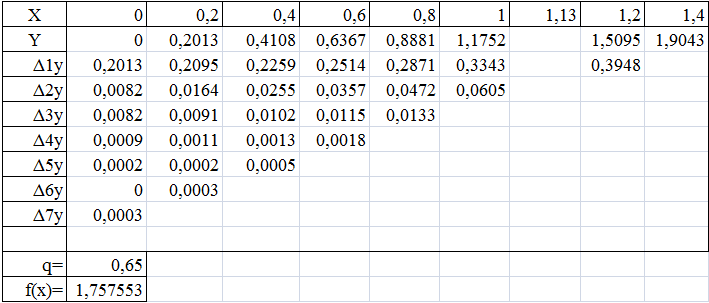
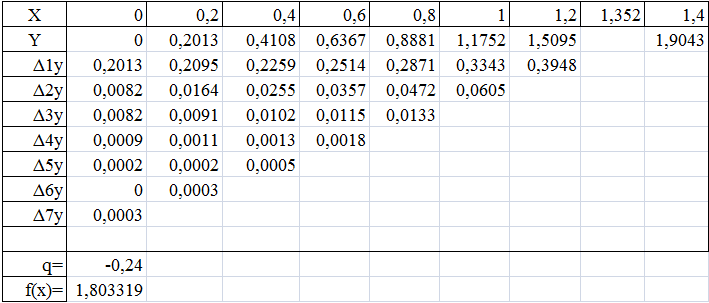
Составляем таблицу центральных разностей
Сравнивать с этим значением
q находится в диапазоне (0,25...0,75)
воспользуемся интерполяционной формулой Бесселя
q находится в диапазоне (0...0,25)
воспользуемся интерполяционной формулой Стирлинга
Воспользуемся первой интерполяционной формулой Ньютона
Воспользуемся второй интерполяционной формулой Ньютона
Сравнивать с этим значением
q находится в диапазоне (0,25...0,75)
воспользуемся интерполяционной формулой Бесселя
q находится в диапазоне (0...0,25)
воспользуемся интерполяционной формулой Стирлинга
Воспользуемся первой интерполяционной формулой Ньютона
Воспользуемся второй интерполяционной формулой Ньютона
Вывод: в процессе выполнения 1 лабораторной работы были рассмотрены различные способы поиска значения заданной функции в точках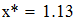 
и .
Сравнительная точность используемых методов оказалась весьма высока.
Численное дифференциирование
1. В точках х* и х** из ЛР№1 вычислить произодную функции, дифференциируя интерполяционные формулы.
2. Создать таблицу с приближеннымизначениями f`(x), которые находим по формулам
а) первого порядка точности
б) второго порядка точности
1. Дифференциируем интерполяционные формулы
Находим значение f `(x) для
Дифференциируем первую формулу Ньютона
Дифференциируем вторую формулу Ньютона
Дифференциируем интерполяционную формулу Стирлинга
Дифференциируем интерполяционную формулу Бесселя
Находим значение f `(x) для
Дифференциируем первую формулу Ньютона
Дифференциируем вторую формулу Ньютона
Дифференциируем интерполяционную формулу Стирлинга
Дифференциируем интерполяционную формулу Бесселя
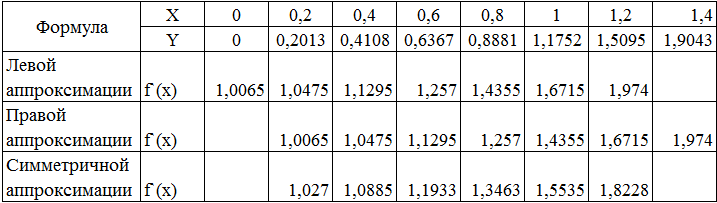
2. Используя формулы перого и второго порядка точности, находим приближенные значения f `(x) и заносим их значения в таблицу
Формулы левой аппроксимации
Формулы правой аппроксимации
Формулы второго порядка точности:
Вывод: В ходе выполнения лабораторной работы нами были дифференцированы интерполяционные формулы представленные в первой лабораторной работе и найдены значения производных в точках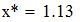 
и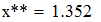 
. Также были найдены значения производной в узловых точках, используя методы первого и второго порядка точности.
Вычислить интеграл с точностью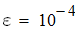 
методами прямоугольников, трапеций и Симпсона.
Вычисляем интеграл методом прямоугольников
Находим предельное значение h из формулы глобальной погрешности квадратурной формулы прямоугольников
Находим минимальное количество ключеыфх точек
Выбираем значение ключевых точек равным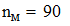 
. Исходя из этого h равно:
Находим значение подинтегрального выражения в ключевых точках и заносим данные в таблицу
2. Вычисляем интеграл методом трапеций.
Находим предельное значение h из формулы глобальной погрешности формулы трапеций
Находим минимальное количество ключеыфх точек
Выбираем значение ключевых точек равным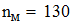 
. Исходя из этого h равно:
Находим значение подинтегрального выражения в ключевых точках и заносим данные в таблицу
3. Вычисляем интеграл методом Симпсона
Находим значение шага сетки h при количестве узловых точек
Находим значение подинтегрального выражения в ключевых точках и заносим данные в таблицу.
Находим центральные разности до второго порядка (необходимо для определения глобальной погрешности)
оценка глобальной погрешности
Вывод: в ходе выполнения лабораторно работы был вычислен интеграл с точностью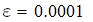 
методом прямоугольников, трапеций и метода Симпсона.
