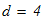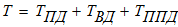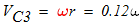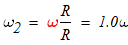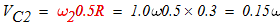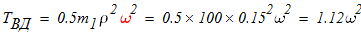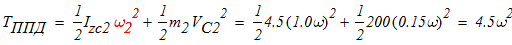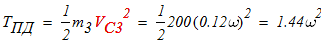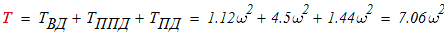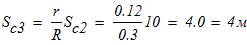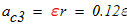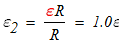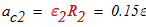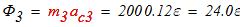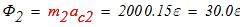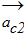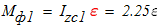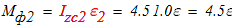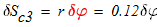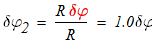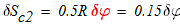Артикул: мех8
Автор решения: admin
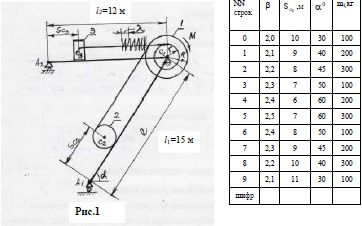
Механика (теоретическая механика и сопротивление материалов) Вычислить: Скорости точек С2 и С3, а также угловые скорости блока 1 и катка 2 в тот момент…
Механика (теоретическая механика и сопротивление материалов)
Вычислить:
-
Скорости точек С2 и С3, а также угловые скорости блока 1 и катка 2 в тот момент времени, когда центр тяжести С2 был смещен на расстояние Sc от опоры А1, а центр тяжести С3 был смещен на расстояние Sc3м от опоры А2..
-
Ускорения точек С2 и С3, а также угловые ускорения блока 1 и катка 2 в тот момент времени, когда их центры тяжести С2 и С3 были смещены на расстояния Sc2 и Sc3 м, соответственно.
-
Время, в течение которого центр тяжести груза 3 (точка С3) переместился на расстояние Sc3 м от опоры А2.
-
Величину минимального значения коэффициента трения скольжения ƒтр2 между катком 2 и брусьями А1С1.
-
Величину максимальной деформации сжатия цилиндрической винтовой пружины λм в момент остановки груза 3.
-
Диаметр проволоки, из которой изготовлена пружина, если средний диаметр её витка равен D=0,2 м, допускаемое напряжение на срез равно [τ]=150 МПа, жесткость пружины равна 50 кН/м.
-
Динамические реакции внешних и внутренних связей в тот момент времени, когда центры тяжести катка 2 и груза 3 смещены на расстояния Sc2 и Sc3 от опор А1 и А2, соответственно. Принять l=15м.
-
Из условия прочности при поперечном изгибе подобрать прочные размеры поперечного сечения бруса А2С1, считая, что он изготовлен из двух швеллеров, опирающихся тыльной стороной на опоры А2 и С1.
Считать, что наибольший изгибающий момент возникает в опасном сечении, располагающемся на расстоянии (Sc3 + 1 м) от опоры А2. Принять допускаемое нормальное напряжение на изгиб стальной детали равным [σ]= 160 МПа.
9. Из условия прочности на разрыв рассчитать диаметр тросов, соединяющих блок 1 с катком 2 и грузом 3, приняв допускаемое напряжение на разрыв [σ]=100 МПа
в каталог
Для, того, чтобы помочь решить ваш вариант, необходимо нажать "Заказать похожую задачу" и указать свой номер варианта, либо указать ваши исходные данные для расчета.
Часть готового решения
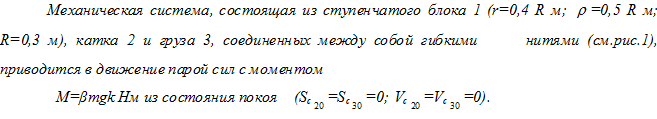
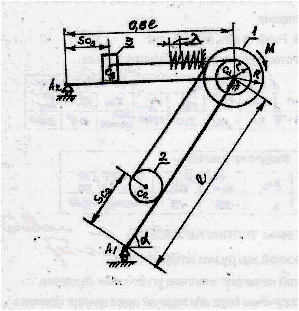
Дано:
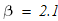
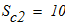
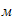
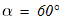
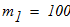
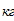
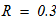
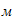
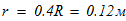
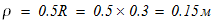
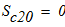
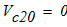
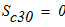
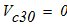
масса катка
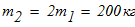
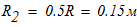
масса груза
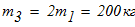
коэффициент трения скольжения между грузом 3 и брусьями А2С1 равен
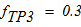
коэффициент трения качения катка 2 по брусьям А1С1 равен
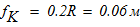
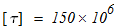
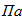
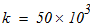
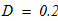
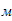
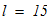
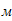
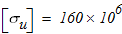
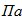
Вычислить:
1. Скорости точек С2 и С3, а также угловые скорости блока 1 и катка 2 в тот момент времени, когда их центры тяжести С2 и С3 были смещены на расстояния Sc2 и Sc3 м от левой опоры.
2.Ускорения точек С2 и С3, а также угловые ускорения блока 1 и катка 2 в тот момент времени, когда их центры тяжести С2 и С3 были смещены на расстояния Sc
3.Время, в течение которого центр тяжести груза 3 (точка С3) переместился на расстояние Sc
4.Величину минимального значения коэффициента трения скольжения ƒтр2 между катком 2 и брусьями А1С1.
5.Величину максимального значения сжатия цилиндрической винтовой пружины λм при статическом сжатии её.
6.Диаметр проволоки, из которой изготовлена пружина, если средний диаметр её витка равен D=0,2 м, допускаемое напряжение на срез равно [τ]=150 МПа, жесткость равна 50 кН/м.
7.Динамические реакции внешних и внутренних связей в тот момент времени, когда центры тяжести катка 2 и груза 3 смещены на расстояния Sc2 и Sc3 от левых опор соответственно.
Решение:
1.Вычерчиваем расчетную схему в крупном масштабе.
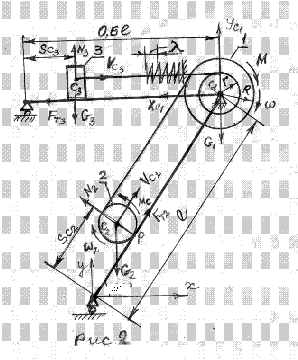
2.Выбираем удобную для расчета плоскую декартову систему координат А1xy.
3. Расставляем в расчетной схеме активные силы:
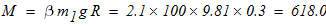
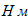
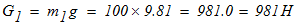
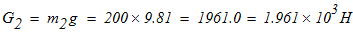
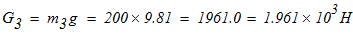
4.Отбрасываем” внешние связи, а действие их на рассматриваемые тела (груз 3, каток 2 и блок 1) заменяем соответствующими реакциями:
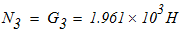
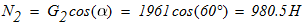
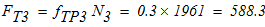
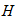
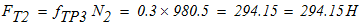
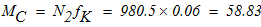
5. Вычисление скоростей.
Воспользуемся теоремой об изменении кинетической энергии механической системы:
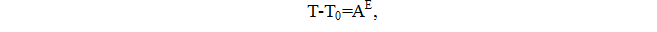
где
Т - кинетическая энергия механической системы в данный момент времени, Дж;
Т0 - кинетическая энергия механической системы в начальный момент времени, Дж;
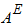
Кинетическая энергия механической системы в любой момент времени складывается из кинетических энергий движущихся тел, которые образуют данную механическую систему. В нашей задаче блок 1 совершает вращательное движение, каток 2 плоскопараллельное движение, груз 3 поступательное движение. Следовательно, кинетическая энергия рассматриваемой механической системы равна:
Так как в любой механической системе тела взаимосвязаны, то скорости всех точек этой системы можно выразить через одну какую-нибудь обобщенную скорость.
Пусть блок 1 вращается с угловой скоростью ώ, 
(т.к. мгновенный центр скоростей катка 2 находится в точке касания Р).
Вычислим кинетическую энергию отдельных тел через обобщенную скорость:
а) блок 1 совершает вращательное движение:
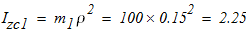
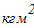
б) каток 2 совершает плоскопараллельное движение:
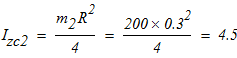
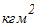
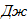
в) груз 3 совершает поступательное движение:
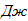
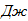
Кинетическая энергия механической системы в начальный момент времени равна нулю, т.к. в начальный момент времени она не двигалась

Вычислим работу внешних активных сил после того, как точки С2 и С3 переместились на расстояние 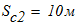
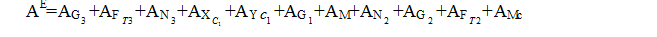
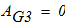
- механическая работа силы тяжести груза 3 равна нулю
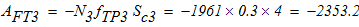
- механическая работа силы трения
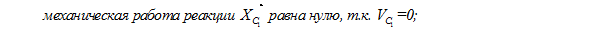
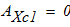
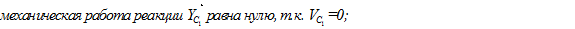
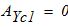
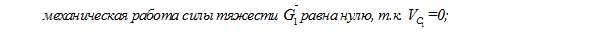
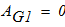
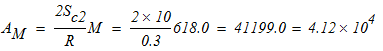
- механическая работа пары сил с моментом М
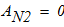
- механическая работа реакции 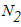
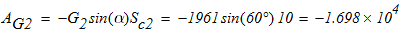
Механическая
работа силы тяжести
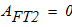
- механическая работа силы трения тела 2 равна 0, так как каток не пробуксосывает
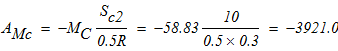
Таким образом, суммарная работа внешних активных сил равна
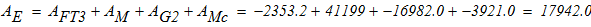
полученные данные подставим в исходную формулу
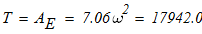
отсюда
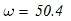
Тогда
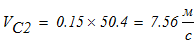
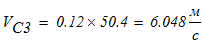
6. Вычисление ускорений.
Вычерчиваем расчетную схему заново.
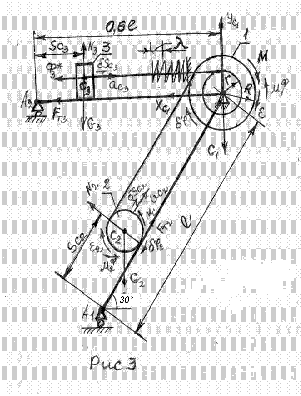
Воспользуемся общим уравнением динамики
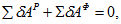
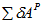
- алгебраическая сумма элементарных работ активных сил на возможных перемещениях точек, к которым они приложены, Дж;
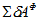
- алгебраическая сумма элементарных работ сил инерции на возможных перемещениях точек, к которым они приложены
При неравномерном движении твердого тела каждая точка его обладает ускорением. Произведение ускорения материальной точки на ее массу в механике называют силой инерции. Прикладывают её к материальной точке и направляют в сторону, противоположную ее ускорению:
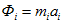
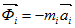
или
Так как твердое тело имеет большое количество материальных частиц, то необходимо научиться вычислять результирующую силу инерции. С этой целью удобно пользоваться методом Пуансо
При поступательном движении твердого тела силы инерции приводятся к одной силе, которая называется главным вектором сил инерции. Вычисляется он по формуле:
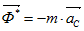
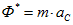
или
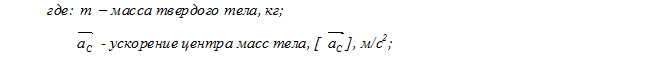
Прикладывается 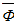
При вращательном движении твердого тела результаты приведения элементарных сил инерции к одному центру зависят от того проходит ось вращения через центр масс или не проходит.
Если ось вращения проходит через центр масс вращающегося тела, то
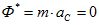
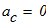
тогда главный вектор сил инерции
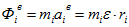
Однако, вращательные составляющие сил инерции
в результате приведения к центру создают суммарный момент сил инерции, называемый главным моментом сил инерции, который вычисляется по формуле:
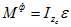

Тогда ускорение точки С3 равно:
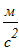
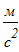
угловое ускорение катка 2 равно:
Ускорение точки С2 равно:
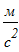
Вычисляем главные векторы сил инерции
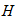
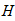
Приложим их соответственно к точкам 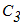
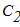
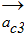
Вычислим главные моменты сил инерции
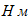
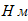

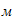
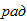
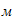
Составим общее уравнение динамики
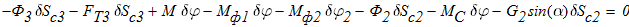
Подставляем числовые значения и получим:

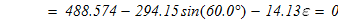
откуда
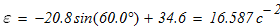
следовательно
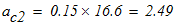
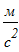
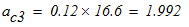
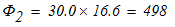
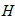
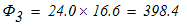
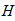
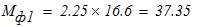
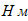
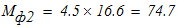
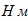
7. Вычислим время, в течение которого центр тяжести груза 3 переместился на расстояние 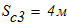
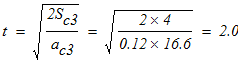
8.Вычисление динамических реакций связей
Расчленим механическую систему на отдельные тела и рассмотрим отдельно равновесие каждого тела

Равновесие груза 3
равновесие катка 2
1)
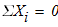
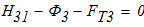
1)
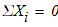
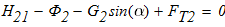
2)
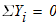
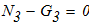
2)
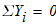
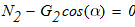
из (2)
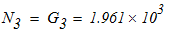
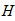
3)
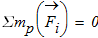
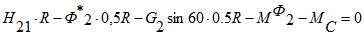
из (1)
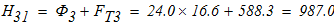
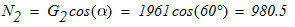
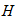
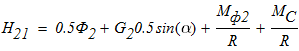
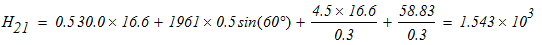
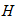
Каток 2 будет двигаться без проскальзывания только в том случае, когда будет выполняться равенство (1). Отсюда следует:
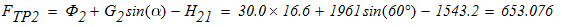
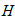
тогда коэффициент трения
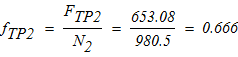
Равновесие блока 1
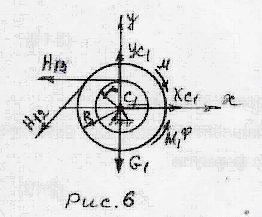
На основании закона о равенстве действия и противодействия запишем
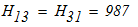
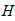
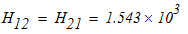
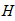
Запишем уравнения равновесия
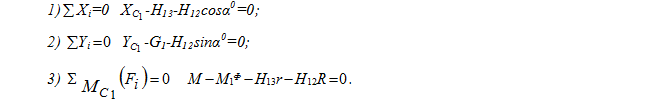
Из (1)
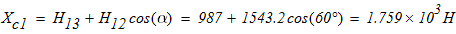
Из (2)
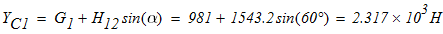
Равенство (3) применим для проверки правильности вычисления реакций связей:
из (3)
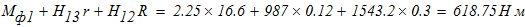
при исходном значении
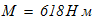
Равенство выполняется. Реакции связей вычислены верно.
9.Расчет пружины.
Для вычисления максимальной деформации пружины воспользуемся принципам возможных перемещений: если механическая система находится в равновесии (в покое), то алгебраическая сумма элементарных работ активных сил, действующих на рассматриваемую механическую систему, на возможных перемещениях точек, к которым они приложены, равна нулю:
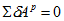
Сообщим блоку 1 возможное перемещение
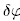
примем его за независимое, и выразим через него перемещение остальных тел и точек (см.рис.3):
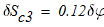
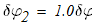
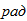
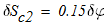
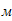
Запишем уравнение работ, активных сил:
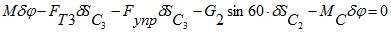

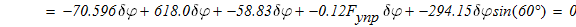
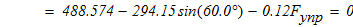

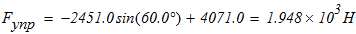
зная жесткость пружины
тогда деформация
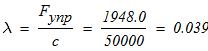
Определим диаметр проволки, из которой может быть сделана пружина
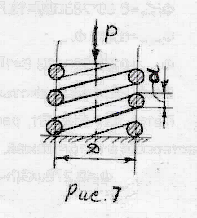

отсюда
принимаем диаметр
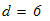
10. Расчет балки.
Будем считать, что брусья А2С1 и А1С1 не связаны между собой жестко. Следовательно, нагрузки, действующие на балку А1С1 не воздействуют на балку А2С1 .
Составим расчетную схему
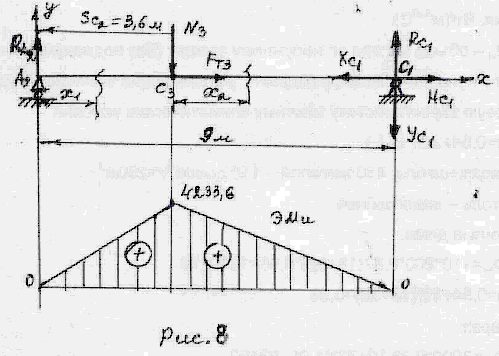
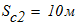
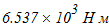
составим уравнения равновесия и вычислим реакции опор:

3)
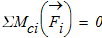
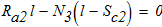
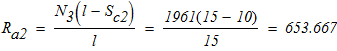
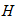
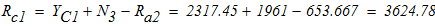
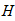
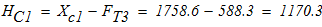
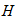
проверка
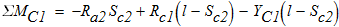
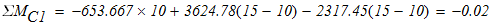
построим эпюру изгибающих моментов:
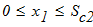
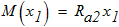
при
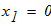
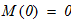
при
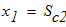
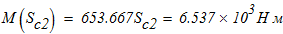
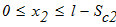
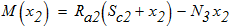
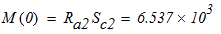
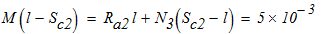
Наибольший изгибающий момент
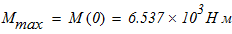

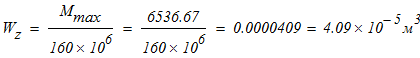
Так как сечение брусьев состоит из двух швеллеров, то для одного швеллера
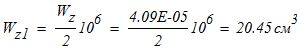
по таблице сортамета выбираем швеллер
Выберем:

Номер швеллера -
момент сопротивления швеллера
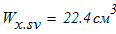
момент инерции
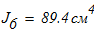
Площадь одного швеллера
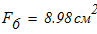

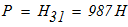
тогда
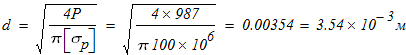
Для обоих случаев принимаем трос с диаметром