РАСЧЕТНО - ПРОЕКТИРОВОЧНАЯ РАБОТА "РАСЧЕТ КОЛОННЫ НА УСТОЙЧИВОСТЬ ИНЖЕНЕРНЫМ МЕТОДОМ"  Задано: расчетная схема колонны; форма составного поперечного…

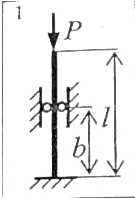
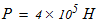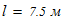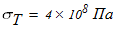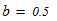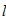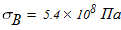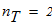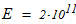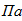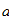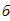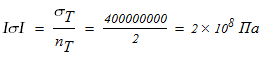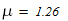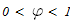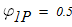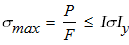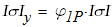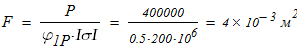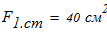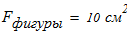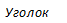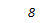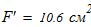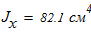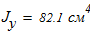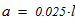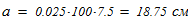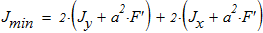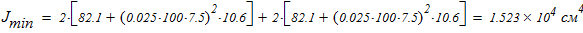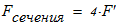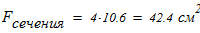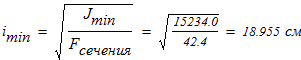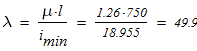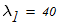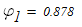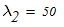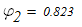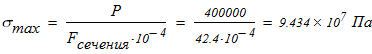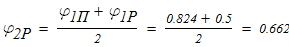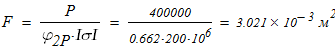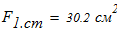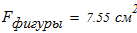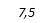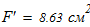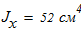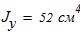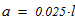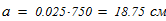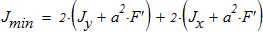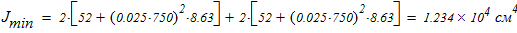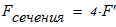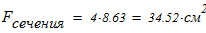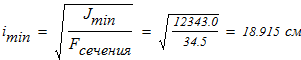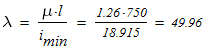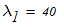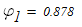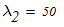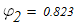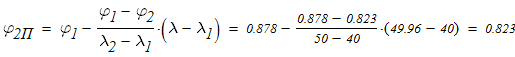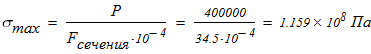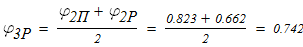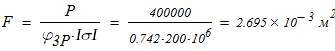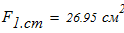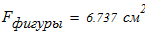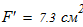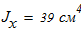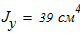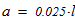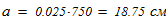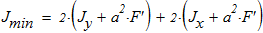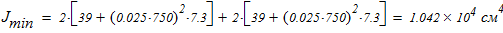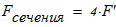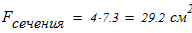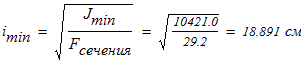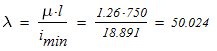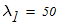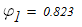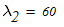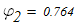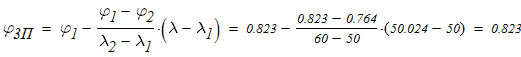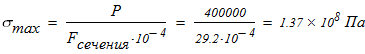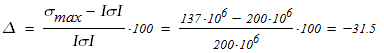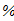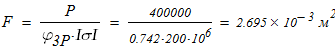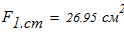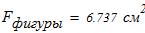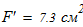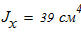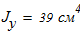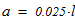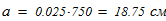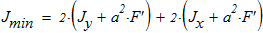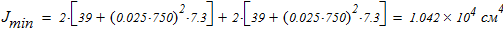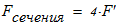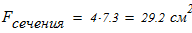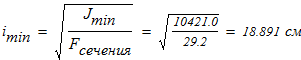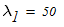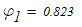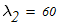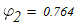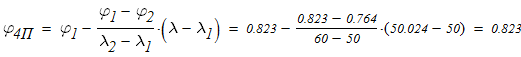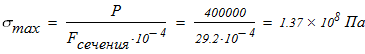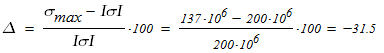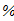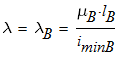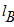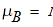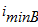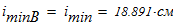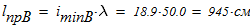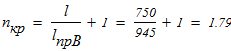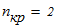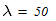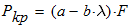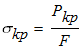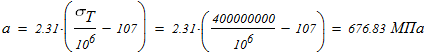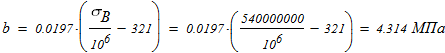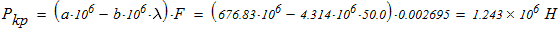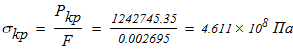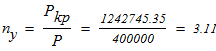Исходные данные для расчета:

Коэфф. запаса прочности

Модуль Юнга

Рис. 1. а - расчетная схема колонны; б - форма поперечного сечения колонны

Решение:

1. Вычисляем допускаемое напряжение на сжатие

2. По таблице П6 находим коэффициент приведения высоты колонны к основному закреплению

3. Поскольку коэффициент продольного изгиба находится в пределах

то в первом приближении принимаем

и из условия устойчивости

Вычисляем площадь составного сечения колонны

4. Из таблицы П5 по расчетной площади

находим блжайшую фигуру -

с табличными значениями

геометрических характеристик

№ профилиля -

Площадь -

Момент инерции по оси Х -

Момент инерции по оси У -

5. Анализ формы составного сечения показывает, что минимальный момент инерции находится по следующей зависимости

6. Вычисляем минимальный радиус инерции составного сечения

определяем гибкость колонны

Из таблицы П.7 определяем при заданном s и величине l необходимые величины

Линейной интерполяцией определяем расчетный коэффициент продольного изгиба

Который существенно отличается от принятого

Второе приближение

Вычисляем площадь составного сечения колонны

4. Из таблицы П5 по расчетной площади

находим блжайшую фигуру -

с табличными значениями

геометрических характеристик

№ профилиля -

Площадь -

Момент инерции по оси Х -

Момент инерции по оси У -

5. Анализ формы составного сечения показывает, что минимальный момент инерции находится по следующей зависимости

6. Вычисляем минимальный радиус инерции составного сечения

определяем гибкость колонны

Из таблицы П.7 определяем при заданном s и величине l необходимые величины

Линейной интерполяцией определяем расчетный коэффициент продольного изгиба

проверим условие выполнения устойчивости

Третье приближение

Вычисляем площадь составного сечения колонны

4. Из таблицы П5 по расчетной площади

находим блжайшую фигуру -

с табличными значениями

геометрических характеристик

№ профилиля -

Площадь -

Момент инерции по оси Х -

Момент инерции по оси У -

5. Анализ формы составного сечения показывает, что минимальный момент инерции находится по следующей зависимости

6. Вычисляем минимальный радиус инерции составного сечения

определяем гибкость колонны

Из таблицы П.7 определяем при заданном s и величине l необходимые величины

Линейной интерполяцией определяем расчетный коэффициент продольного изгиба

проверим условие выполнения устойчивости

Рабочее напряжение меньше допустимого на

Четвертое приблжение

Вычисляем площадь составного сечения колонны

4. Из таблицы П5 по расчетной площади

находим блжайшую фигуру -

с табличными значениями

геометрических характеристик

№ профилиля -

Площадь -

Момент инерции по оси Х -

Момент инерции по оси У -

5. Анализ формы составного сечения показывает, что минимальный момент инерции находится по следующей зависимости

6. Вычисляем минимальный радиус инерции составного сечения

определяем гибкость колонны

Из таблицы П.7 определяем при заданном σ и величине l необходимые величины

Линейной интерполяцией определяем расчетный коэффициент продольного изгиба

проверим условие выполнения устойчивости

Рабочее напряжение меньше допустимого на

Более точно подобрать номер проката для колонны не удалось.

Необходимо, чтобы колонна была устойчива не только в целом, но устойчивыми были ее отдельные части. Условие равноустойчивости колонны и ветвей будет выполнено если гибкости ветвей и колонны будут равны.

- высота ветви, м;

- коэффициент приведения высоты ветви;

- минимальный радиус инерции сечения ветви.

Вычисляем предельную высоту ветви

что меньше высоты колонны. Следовательно для обеспечения устойчивости ветвй и колонны в целом, необходимо предусмотреть определенное число креплений(сварных, болтовых)

Примем

Вычисляем критическую силу. Поскольку гибкость колонны

то используем формулу Ясинского

где

тогда

Находим коэффициент запаса устойчивости у колонны