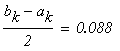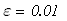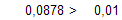Математика → Математические задачи электроэнергетики
Артикул: матем1
Автор решения: admin
Лабораторная работа Численная минимизация функции одной переменной. 1. Выделить отрезок, содержащий точку минимума. 2. Используя прямые и непрямые…
Лабораторная работа
Численная минимизация функции одной переменной.
1. Выделить отрезок, содержащий точку минимума.
2. Используя прямые и непрямые методыминимизации, найти минимум функции y = f(x) на отрезке [a,b], указанном в задании
1. Метод перебора e=0,5
Вычислить N, необходимое для данного е. Сделать выводы.
2. Метод половинного деления (е=0,01 "бета" =2*е)
Определить количество итераций, указать количество вычислений функций f(x)
3. Метод золотого сечения (е = 0,01)
Определить количество итераций, указать количество вычислений функции f(x)
4. Метод касательных (е=0,01)
Определить количество итераций, указать количество вычислений функции f(x) и количество вычисленных производных f`(x)
5. Метод Ньютона (е = 0,01)
В качестве Хо взять Xmin из метода перебора и взять одну из границ отрезка. Указать количество итераций , количество вычислений функции f(x) и количество вычислений производных f`(x)
Сравнить методы по эффективности. Провести сравнение по количеству итераций, количеству вычислений функции f(x) и количеству вычислений производных f`(x)
<в каталог
Как заказать работу?
↓
Добавляем заказ в корзину
↓
Оплачиваем → Сообщаете МНЕ об оплате (зарегистрированным пользователям)
↓
В течении одного рабочего дня высылаю решение на вашу почту или в контакт.
Часть готового решения
ЧАСТЬ ГОТОВОГО РЕШЕНИЯ
Лабораторная работа
1. Выделить отрезок, содержащий точку минимума.
2. Используя прямые и непрямые методы минимизации, найти минимум функции 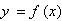
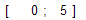
Дано:
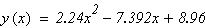
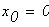
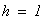
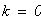
тогда
Решение: 1) пусть
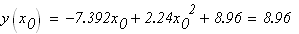
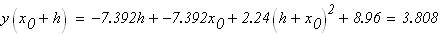
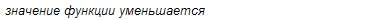
следовательно
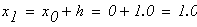
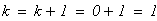
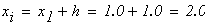
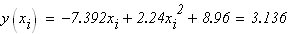
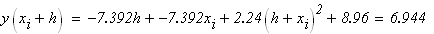

следовательно
отрезок минимума
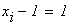
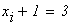
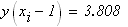
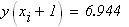
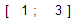
на данном отрезке длиной
расположен минимум функции
графически это выглядит так:
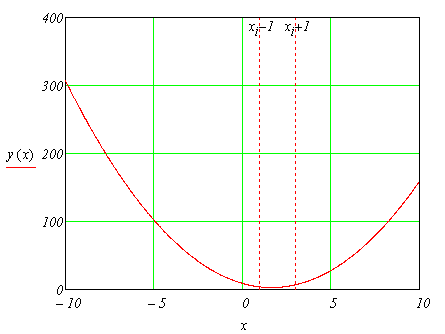
Метод перебора.
Вычислить N, необходимое для данного
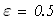
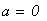
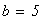
Решение: находим число разбиений N:
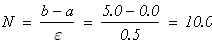
шаг разбиения
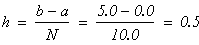
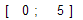
На отрезке
выберем узловые точки 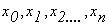
тогда
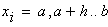
Получим
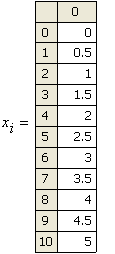
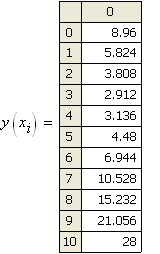
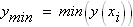
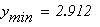
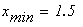
Достоинства метода: 1) применяется, когда не требуется точных решений;
2) легко усваиваемый.
Недостатки метода:
1) Много вычислений;
2)точность вычислений невысокая.
2. Метод половинного деления
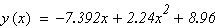
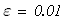
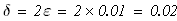
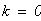
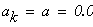
Решение:
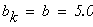
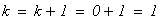
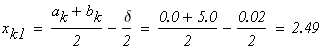
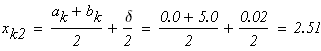
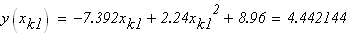
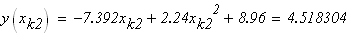
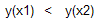
следовательно
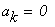
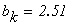
Условие выхода
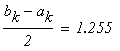
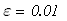
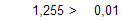
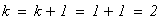
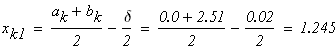
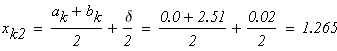
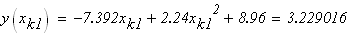
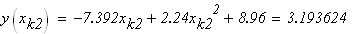
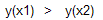
следовательно
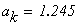
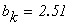
Условие выхода
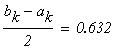
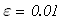
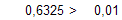
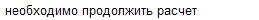
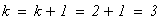
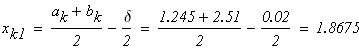
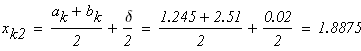
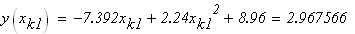
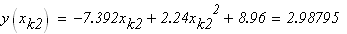
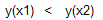
следовательно
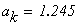
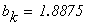
Условие выхода
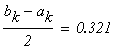
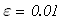
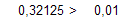
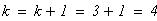
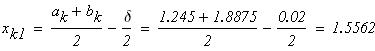
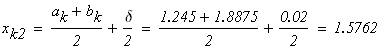
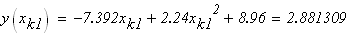
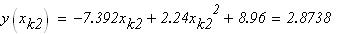
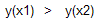
следовательно
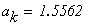
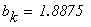
Условие выхода
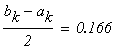
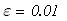
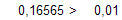
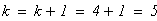
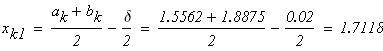
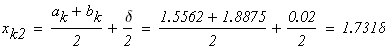
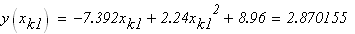
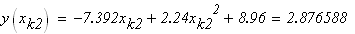
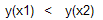
следовательно
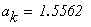
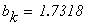
Условие выхода